 |
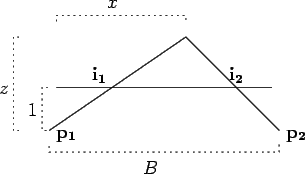
Uma vez na posse de um mapa de disparidade entre imagem esquerda e direita, obtido para câmaras calibradas, a conversão do ponto (u, v, d ) em coordenadas (x, y, z) (num dado referencial) é trivial. Admita-se que as imagens foram previamente rectificadas, seja (u, v, d ) as coordenadas de um pixel na imagem e a respectiva disparidade, e seja B a distância entre os centros de projecção das duas câmaras. Dado que as imagens foram rectificadas, B é simplesmente a coordenada x da descrição do centro de projecção da câmara direita no referencial local da câmara esquerda. Da rectificação sai também que a distância focal (f) de ambas as câmaras é igual e a coordenada cy do ponto principal é também igual. A intersecção segundo x de cada recta com o plano de projecção (no referencial local da câmara esquerda, ver figura 5.4.1) vem dada por
| i1x | = 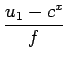 |
|
| i2x | = 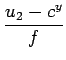 + B + B |
= 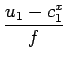 |
||
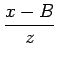 |
= 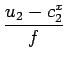 |
| z | = 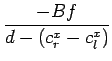 |
|
| x | = z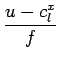 |
|
| y | = z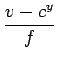 |
Em [14] refere-se a seguinte relação5.4
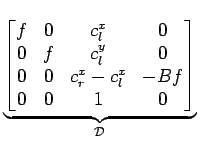
Supondo então que se tem o plano de água
W![]() =
= ![]()
![]()
![]() correspondente ao plano z = 0 (a região
+ corresponde ao semi-espaço com a coordenada z positiva). Este plano pode ser levado para coordenadas de câmara através de 5.4.1 (usando
correspondente ao plano z = 0 (a região
+ corresponde ao semi-espaço com a coordenada z positiva). Este plano pode ser levado para coordenadas de câmara através de 5.4.1 (usando
![]() ) e de seguida para o espaço de disparidade aplicando novamente 5.4.1 (usando
) e de seguida para o espaço de disparidade aplicando novamente 5.4.1 (usando
![]() ). Tem-se assim uma maneira de diferenciar pontos sobre e sob o plano de água no espaço de disparidade. Isto é importante dado que cada imagem apenas é ``válida'' dentro de água (caso se aplique a rectificação de snell) ou fora de água (caso não se aplique a rectificação de snell), obrigando a que cada triplo (u, v, d ) seja reconstruído de maneira diferente em cada caso.
). Tem-se assim uma maneira de diferenciar pontos sobre e sob o plano de água no espaço de disparidade. Isto é importante dado que cada imagem apenas é ``válida'' dentro de água (caso se aplique a rectificação de snell) ou fora de água (caso não se aplique a rectificação de snell), obrigando a que cada triplo (u, v, d ) seja reconstruído de maneira diferente em cada caso.
Para o caso em que se pretende reconstruir objectos submersos, o uso de
![]() é apenas aproximado, sendo o resultado exacto obtido aplicando 4.1.10 e 4.1.11 a cada emparelhamento de pixels, detectando de seguida a intersecção das rectas descritas pelo emparelhamento, como descrito no Apêndice B. Note-se porém que o plano z = 0 não é alterado pela rectificação de snell (a transformação de Snell descrita mapeia o plano da interface nele próprio), pelo que é válido aplicar 5.4.1 para decidir quais os pixels sobre e sob o plano de água, como descrito no parágrafo anterior.
é apenas aproximado, sendo o resultado exacto obtido aplicando 4.1.10 e 4.1.11 a cada emparelhamento de pixels, detectando de seguida a intersecção das rectas descritas pelo emparelhamento, como descrito no Apêndice B. Note-se porém que o plano z = 0 não é alterado pela rectificação de snell (a transformação de Snell descrita mapeia o plano da interface nele próprio), pelo que é válido aplicar 5.4.1 para decidir quais os pixels sobre e sob o plano de água, como descrito no parágrafo anterior.
De forma a facilitar a visualização da reconstrução, desenvolveu-se uma aplicação em C usando OpenGL (com interface para Matlab), permitindo a navegação no ambiente. Na figura 5.4.2 apresentam-se imagens da aplicação a correr. Destaca-se que é possível uma navegação suave usando em combinação o rato e o teclado.
Para testar a viabilidade da aproximação de snell, colocou-se um par de câmaras a cerca de 1.3m de altura relativamente ao interface (ver figura 5.4.3) e reconstruiu-se um objecto planar (colocado paralelo ao interface) a várias profundidades. O erro de reconstrução obtido quando se usa apenas a matriz
![]() apresenta-se na figura 5.4.4. Como seria de esperar, o erro aumenta com a profundidade a que o plano é colocado e com o ângulo que o raio de luz faz face à normal do interface. Em particular, repare-se nos cantos superiores onde muito ruído se faz notar devido a erros de rectificação provocados pelo ângulo já elevado dos raios de luz incidentes face à normal do interface (cerca de 25 graus para o canto superior direito da imagem da câmara esquerda). Não contando com este factor e olhando para o pior caso (plano a 1.5 metros de profundidade) observam-se erros de cerca de 25 centímetros perto dos cantos inferiores da imagem (ângulo incidente de cerca de 15 graus para o canto inferior direito da imagem obtida pela câmara esquerda). Dada a posição do plano face às câmaras, é um erro relativo5.5 de 10%. Este exemplo serve para mostrar que a rectificação a partir da aproximação de snell de primeira ordem apenas é válida numa vizinhança próxima da normal à interface. Nas imagens apresentadas esta vizinhança está centrada no pixel
(u, v) = (424, 363).
apresenta-se na figura 5.4.4. Como seria de esperar, o erro aumenta com a profundidade a que o plano é colocado e com o ângulo que o raio de luz faz face à normal do interface. Em particular, repare-se nos cantos superiores onde muito ruído se faz notar devido a erros de rectificação provocados pelo ângulo já elevado dos raios de luz incidentes face à normal do interface (cerca de 25 graus para o canto superior direito da imagem da câmara esquerda). Não contando com este factor e olhando para o pior caso (plano a 1.5 metros de profundidade) observam-se erros de cerca de 25 centímetros perto dos cantos inferiores da imagem (ângulo incidente de cerca de 15 graus para o canto inferior direito da imagem obtida pela câmara esquerda). Dada a posição do plano face às câmaras, é um erro relativo5.5 de 10%. Este exemplo serve para mostrar que a rectificação a partir da aproximação de snell de primeira ordem apenas é válida numa vizinhança próxima da normal à interface. Nas imagens apresentadas esta vizinhança está centrada no pixel
(u, v) = (424, 363).
|
![\includegraphics[width=200pt]{erro_reconstruccao_plano_01.eps}](img321.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_50.eps}](img322.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_100.eps}](img323.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_150.eps}](img324.gif) |
Usando os mesmos mapas de disparidade obtidos acima, leva-se agora em consideração a existência da interface na reconstrução (ver figura 5.4.5). Os pontos tridimensionais são agora obtidos através da intersecção de dois raios refractados pela interface. Embora a existência de ruído seja ainda evidente nos cantos superiores (dado que não se mexeu nos mapas de disparidade), o erro diminui significativamente no pior caso passando a ser cerca de 3 centímetros a uma profundidade de 1.5 metros, resultando num erro relativo de pouco mais de 1%. Repare-se que este valor é o erro esperado devido à quantização da disparidade para a distância em questão.
![\includegraphics[width=200pt]{erro_reconstruccao_plano_01_corrected.eps}](img325.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_50_corrected.eps}](img326.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_100_corrected.eps}](img327.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_150_corrected.eps}](img328.gif) |
Numa tentativa de diminuir o ruído existente nos exemplos anteriores, obteve-se um mapa de disparidade bidimensional (segundo u e v) usando o algoritmo de stereo denso semelhante ao das coordenadas cíclicas descrito na secção 5.3.3. Os resultados da aplicação deste algoritmo às imagens de planos anteriores apresentam-se na figura 5.4.6. Conclui-se que o algoritmo converge adequadamente nestas imagens, não havendo em qualquer imagem erros superiores aos cerca de 3 centímetros devido à quantização.
![\includegraphics[width=200pt]{erro_reconstruccao_plano_01_corrected2.eps}](img329.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_50_corrected2.eps}](img330.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_100_corrected2.eps}](img331.gif)
![\includegraphics[width=200pt]{erro_reconstruccao_plano_150_corrected2.eps}](img332.gif) |