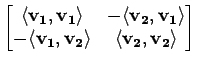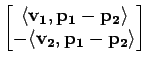Intersecção de Duas Rectas Descritas Parametricamente
Considere-se agora o problema de encontrar a intersecção de duas rectas num espaço N dimensional com a possibilidade de existência de erros nos parâmetros. Pretende-se portanto encontrar o ponto médio do segmento de recta mais curto que una um ponto em cada recta. Se supormos que cada recta é parametrizada por
r(t) = p + tv
onde
p é um ponto N dimensional e
v é um vector também N dimensional. O funcional de custo a minimizar de forma a achar t1 e t2 é portanto
E =
 r1
r1(
t1) -
r2(
t2)

=
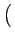 p1l
p1l +
t1v1l -
p2l -
t2v2l
Uma vez mais é condição necessária e, para este funcional de custo, suficiente de optimalidade
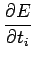
= 2
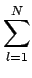 vil
vil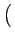 p1l
p1l +
t1v1l -
p2l -
t2v2l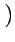
= 0
i = 1, 2
Esta equação têm a interpretação geométrica de o segmento de recta que une as duas rectas ter que ser perpendicular a cada uma delas. A equação pode ser escrita em forma matricial usando o produto interno usual
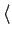 . , .
. , . 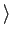 :
Após resolvido o sistema (que apenas não terá solução caso os vectores sejam paralelos), a solução pretendida vem dada pelo ponto médio do segmento de recta
:
Após resolvido o sistema (que apenas não terá solução caso os vectores sejam paralelos), a solução pretendida vem dada pelo ponto médio do segmento de recta
q =
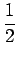
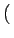 p1
p1 +
t1v1 +
p2 +
t2v2
Este
q será o nosso ponto tridimensional reconstruído.
Ricardo
2004-11-06