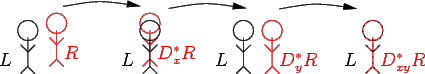Contents of Emparelhamento Denso Bidimensional

Emparelhamento Denso Bidimensional

Dada a distorção introduzida pela água, será necessário obter mapas de disparidade não só segundo u, mas também segundo v^5.3. Assumindo à partida que a disparidade segundo v é pequena e varia continuamente (algo que não se pode assumir segundo u), pode-se pensar numa extensão ao algoritmo anterior, englobando-o em algo semelhante ao conhecido método das coordenadas cíclicas

Se se pensar que os mapas de disparidade definem uma função que indica qual o pixel na imagem direita que melhor descreve um dado pixel na imagem esquerda, uma vez calculados estes mapas pode-se obter uma aproximação da imagem esquerda ``puxando'' os pixels correspondentes da imagem direita. Se D for um elemento do conjunto dos mapas de disparidade (note-se que nesta representação está-se a juntar disparidade segundo u e v) pode-se pensar na acção deste sobre o conjunto das imagens e será representada por L' = D^*R (L' é o resultado da acção de D sobre R, ou seja, L' é a imagem formada ``puxando'' a imagem R por D). É então possivel a composição destes mapas da maneira usual. Se se definir também a operação de transposição de imagem de forma semelhante à transposição de matrizes (cuja representação continua a ser ^T), o algoritmo que se propõe é o seguinte (ver figura 5.3.4)

D_x	= sun(L, R)
D_y	= sun(L^T,(D_x^*R)^T)
D_x	= sun(L, D_y^*R)
D_xy	= D_x`o`D_y

**Figura:** Ilustração do algoritmo de coordenadas cíclicas. Primeiro uma estimativa da disparidade segundo u é obtida, sendo usada para se obter a disparidade segundo v (que deverá ser próxima de zero para que o primeiro passo tenha significado). Uma vez que se saiba a disparidade segundo v, recalcula-se a disparidade segundo u.
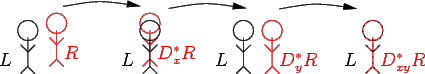$\begin{figure}\center \input{coordenadas_ciclicas.pstex_t} \end{figure}$

Onde sun(^.,^.) designa uma aplicação do algoritmo do Sun. Na figura 5.3.5 apresentam-se os mapas de disparidade obtidos quando se aplica este algoritmo a um plano submerso.

**Figura:** Mapas de disparidade obtidos com o algoritmo de coordenadas cíclicas aplicado a um plano submerso (plano a 1.5m de profundidade e câmaras a cerca de 1.3m acima do interface). Como indicado, à esquerda apresenta-se o mapa de disparidade segundo X, à direita o mapa de disparidade segundo Y.
$\includegraphics[width=200pt]{plane_dx.eps}$ $\includegraphics[width=200pt]{plane_dy.eps}$

Porém será também necessário emparelhar imagens onde tanto a disparidade segundo u como a disparidade segundo v são elevadas. Outra maneira possível de se conseguir emparelhamento, consiste em procurar numa região da imagem 2, algo que se assemelhe a um dado padrão da imagem 1. Se C(u, v, du, dv, n) corresponder agora a uma medida de distância, por exemplo o simétrico do valor da correlação cruzada normalizada após removida a média (em inglês zero mean normalized cross-correlation) de uma janela de tamanho (2n + 1)x(2n + 1) centrada em (u, v) numa imagem e em (u + du, v + dv) na outra, pode-se então pensar no emparelhamento de um pixel (u, v) na primeira imagem, como sendo:

(du^, dv^)_uv = arg $\displaystyle \underset{(du,dv)}{\textrm{max}}$	C(u, v, du, dv, n)
s.t.	du $\displaystyle \in$ I_u
	dv $\displaystyle \in$ I_v

(5.3.2)

para um dado tamanho de janela n, onde I_u e I_v são os intervalos onde du e dv são permitidos variar. Para uma imagem de dimensões MxN, fica-se com MN problemas de optimização distintos, cada um com complexidade da ordem de I_uI_v. Note-se que neste problema não se usam quaisquer restrições de suavidade ou de ordem, usando apenas os limites de procura descritos por I_u e I_v. Para simplificar a procura, usam-se técnicas de multi-resolução, começando inicialmente em imagens de dimensão bastante reduzida e propagando os resultados (com possiveis erros) até à imagem de tamanho real.

Este algoritmo é bastante simples mas pouco robusto, sendo apenas usado para se conseguir o emparelhamento entre as imagens sem e com interface, necessário para a estimação da interface. Note-se que o algoritmo do Sun neste caso não pode ser usado dado que não se tem restrição epipolar (nem algo próximo). Um exemplo dos resultados obtidos apresenta-se na figura 5.3.6.

Com estes algoritmos pretende-se apenas provar a veracidade do algoritmo de estimação da interface, não sendo de interesse a utilidade/robustez noutras imagens para além das apresentadas.

**Figura 5.3.6:** Mapas de disparidade obtidos com o algoritmo de procura exaustiva aplicado a uma bolha de água com 1dm de espessura máxima sobre um plano a cerca de 2.8m de distância. Como indicado, à esquerda apresenta-se o mapa de disparidade segundo x, à direita o mapa de disparidade segundo v.
$\includegraphics[width=200pt]{bolha_dx.eps}$ $\includegraphics[width=200pt]{bolha_dy.eps}$

Ricardo 2004-11-06