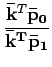A rectificação então consiste em projectar os pontos do plano de retina sobre o plano de interface, alterar os parâmetros da câmara e reprojectar no novo plano de retina. Suponha-se que se pretende projectar um ponto
p1 sobre um plano
 usando como centro de projecção um ponto
p0. Como visto em [4], uma recta em
usando como centro de projecção um ponto
p0. Como visto em [4], uma recta em
 3 pode ser descrita por
e pretende-se encontrar o ponto desta recta que pertence ao plano
3 pode ser descrita por
e pretende-se encontrar o ponto desta recta que pertence ao plano
 . Assim pretende-se encontrar
. Assim pretende-se encontrar 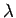 tal que
tal que
O ponto projectado sobre o plano (que se designará por
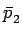 ) será então
Como se trabalha no espaço projectivo e
) será então
Como se trabalha no espaço projectivo e
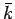 T
T é escalar, usa-se a relação de equivalência para escrever o anterior como
é escalar, usa-se a relação de equivalência para escrever o anterior como
onde
I designa a matriz identidade. Tem-se assim uma matriz de projeção parametrizada pelo centro de projecção e pelo plano onde se pretende projectar. Em particular, para o plano z = 0
![$ \left(\vphantom{\mathbf{\bar{k}}=\left [\begin{array}{ccccccc}0&0&1&0\end{array}\right ]^T}\right.$](img176.gif)
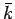 =
= 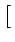
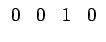
![$ \left.\vphantom{\begin{array}{ccccccc}0&0&1&0\end{array}}\right]^{T}_{}$](img179.gif)
![$ \left.\vphantom{\mathbf{\bar{k}}=\left [\begin{array}{ccccccc}0&0&1&0\end{array}\right ]^T}\right)$](img180.gif) a matriz de projecção toma a forma
a matriz de projecção toma a forma
Assim, assumindo que as imagens foram previamente corrigidas de forma a não apresentarem distorção ocular, é possível corrigir as imagens de acordo com a aproximação de snell de primeira ordem aplicando a seguinte homografia:
H = 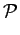 2M(p0) 2M(p0)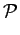 1-1 1-1 |
(4.1.9) |
Onde
 1 é a matriz de projecção da câmara original,
1 é a matriz de projecção da câmara original,
 2 é a matriz de projecção da câmara com os parâmetros intrínsecos e extrínsecos alterados (como descrito na secção 4.1.3, em particular pela equação 4.1.7),
M(p0) é a matriz descrita na equação 4.1.8, onde
p0 é o centro de projecção da câmara original.
2 é a matriz de projecção da câmara com os parâmetros intrínsecos e extrínsecos alterados (como descrito na secção 4.1.3, em particular pela equação 4.1.7),
M(p0) é a matriz descrita na equação 4.1.8, onde
p0 é o centro de projecção da câmara original.
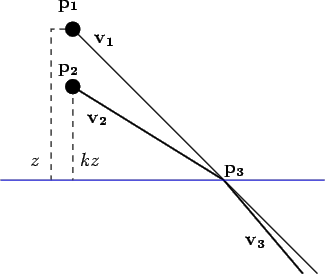
Note-se que após esta transformação, as equações 4.1.3-4.1.5 deixam de descrever o efeito desejado, não permitindo portanto o seu uso na triangulação necessária no algortimo de reconstrução. De seguida corrigem-se estas equações, de forma a serem válidas para imagens previamente transformadas pelo processo anterior. Como se apresenta na figura 4.1.4, pretende-se para cada pixel de cada imagem calcular o par
(p3,v3) a partir de
(p1,v1), que define o caminho seguido pela luz debaixo de água.
Figura:
Ilustração do erro de reconstrução devido à aproximação de snell. Repare-se que a trajectória exacta seguida pelo feixe de luz debaixo de água será segundo
v3 e não segundo
v1.
 |
Assim, definindo parametricamente uma recta através de
p1 e
v1 calcula-se a intersecção desta com o plano de interface z = 0:
Como se sabe, a aproximação de snell deslocou o centro de projecção de cada câmara segundo a transformação 4.1.6, logo:
e portanto
Para o par
(p2,v2) as equações 4.1.3-4.1.5 são novamente válidas e ao aplicá-las, levando em consideração os sinais das grandezas e que
a = sgn(
a)
. |
a|= sgn(
a)
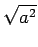
obtém-se
Ricardo
2004-11-06