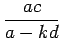Pretende-se agora traçar o caminho percorrido pela luz na sua ida de um ponto
p1 (no ambiente 1) a um ponto
p2 (no ambiente 2), havendo entre eles uma interface planar. Sem perda de generalidade e de forma a facilitar os cálculos, pode-se calcular a solução para
![]() 2, sendo trivialmente generalizável para
2, sendo trivialmente generalizável para
![]() 3 por meio de uma simples mudança de coordenadas antes, e a respectiva inversa após os cálculos que se seguem. Da mesma forma, assume-se que o interface se encontra no plano y = 0 (uma vez mais faz-se notar que estamos em
3 por meio de uma simples mudança de coordenadas antes, e a respectiva inversa após os cálculos que se seguem. Da mesma forma, assume-se que o interface se encontra no plano y = 0 (uma vez mais faz-se notar que estamos em
![]() 2) e o ponto
p1 tem abcissa nula. Ver figura C.1.
2) e o ponto
p1 tem abcissa nula. Ver figura C.1.
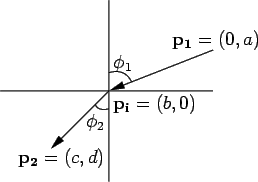 |
| = arctan |
||
| = arctan |
Aplicando as expressões 4.1.1 e 4.1.2 obtém-se
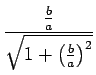 = k2
= k2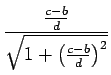
Apesar de não servir de prova, testes numéricos indicam que existe apenas uma raiz real compreendida no intervalo [0, c]. Embora exista uma solução em forma fechada para as raízes de polinómios de quarta ordem, é bastante mais simples calculá-las usando métodos iterativos. Uma implementação usando o método de Newton (adaptado a polinómios como descrito em [17], também conhecido por método de Bierge-Vieta) foi testada, gerando cerca de 10 dígitos significativos em 4 ou 5 iterações. A estimativa inicial é fornecida pela aproximação de Taylor de primeira ordem mencionada na secção 4.1.2C.1:
![$\displaystyle \underbrace{{\left [\begin{array}{ccccccc}kv_1^x \\ v_1^y\end{array}\right ]}}_{{\mathbf{v_2}}}^{}\,$](img431.gif) = p2
= p2
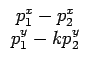
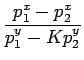 =
=