Aproximação de Taylor de Primeira Ordem
Dada a complexidade da expressão 4.1.5, aproxima-se o resultado exacto pela sua expansão em série de Taylor, da qual se aproveita apenas os termos de primeira ordem4.3:
f (
p)
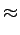 f
f (
a) +
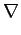 f
f (
a)
T(
p -
a),
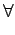 f
f :
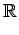 N
N 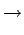
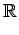
Como se posicionarão as câmaras a olhar segundo uma direcção próxima da vertical no sentido negativo do eixo, calcula-se a expansão em série da função
v2z(v), em torno do vector
va = 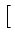
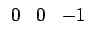
![$ \left.\vphantom{\begin{array}{ccccccc}0&0&-1\end{array}}\right]^{T}_{}$](img117.gif) . O gradiente é então
e aplicando a lei de Snell ao vector
va obtém-se
vz2(va) = - 1, concluindo-se que a aproximação de Taylor de primeira ordem é:
ou seja
. O gradiente é então
e aplicando a lei de Snell ao vector
va obtém-se
vz2(va) = - 1, concluindo-se que a aproximação de Taylor de primeira ordem é:
ou seja
Figura:
Comparação entre o ângulo de refracção aproximado por uma série de Taylor de primeira ordem e o ângulo obtido pela lei de Snell quando aplicado a uma interface ar/água (k = 1/1.33).
![\includegraphics[width=200pt]{erro_approx_linear_snell.eps}](img143.gif)
![\includegraphics[width=200pt]{erro_approx_linear_snell_1.eps}](img144.gif) |
O erro cometido pela aproximação apresenta-se na figura 4.1.2. Não é difícil de concluir que esta aproximação pode ser implementada através de uma mudança dos parâmetros da câmara, como se descreve na secção seguinte. Só a título informativo e dando alguma credibilidade à aproximação usada, em óptica chama-se à aproximação de primeira ordem à lei de Snell
k1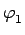
=
k2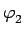
de aproximação paraxial e é frequentemente usada (ver por exemplo [6] e [7]).
Ricardo
2004-11-06
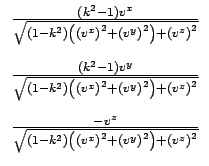
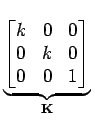 v1
v1
![\includegraphics[width=200pt]{erro_approx_linear_snell.eps}](img143.gif)
![\includegraphics[width=200pt]{erro_approx_linear_snell_1.eps}](img144.gif)