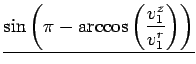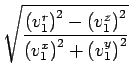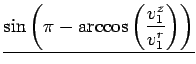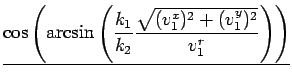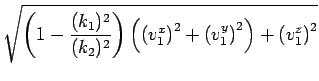Partindo da transformação em coordenadas esféricas:
| r |
= |
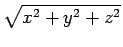 |
|
 |
= |
arctan x, y x, y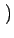 |
|
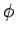 |
= |
arccos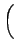 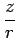 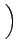 |
|
e a respectiva transformação inversa
| x |
= |
r cos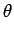 sin sin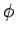 |
|
| y |
= |
r sin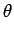 sin sin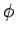 |
|
| z |
= |
r cos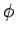 |
|
para
r 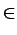
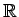 0+,
0+,
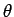
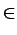 [0, 2
[0, 2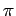 [ e
[ e
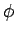
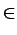 [0,
[0, 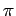 [. Pode-se então descrever um vector
v =
[. Pode-se então descrever um vector
v = 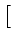
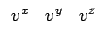
![$ \left.\vphantom{\begin{array}{ccccccc}v^x &v^y &v^z\end{array}}\right]^{T}_{}$](img75.gif) em coordenadas esféricas vr, v
em coordenadas esféricas vr, v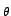 e v
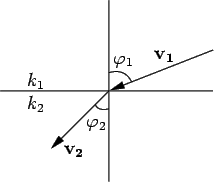
e v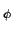 . Assumindo uma interface planar em z = 0, aplicar a lei de Snell
. Assumindo uma interface planar em z = 0, aplicar a lei de Snell
k1sin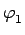 = k2sin = k2sin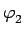 |
(4.1.1) |
onde ki são os índices de refracção do meio i e os ângulos 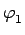 e
e 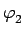 são medidos em relação à normal à interface como mostra a figura 4.1.1, permite calcular a coordenada v
são medidos em relação à normal à interface como mostra a figura 4.1.1, permite calcular a coordenada v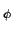 do vector que define a trajectória do raio de luz após atravessar o interface. Se se designar por
vi o vector no ambiente i4.1, tem-se então
do vector que define a trajectória do raio de luz após atravessar o interface. Se se designar por
vi o vector no ambiente i4.1, tem-se então
Figura 4.1.1:
Ilustração dos ângulos considerados na lei de snell.
 |
permanecendo as restantes coordenadas esféricas inalteradas (
vr2 = vr1 e
v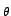 2 = v
2 = v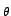 1).
1).
Interpretando geometricamente as funções trigonométricas permite apresentar as seguintes implicações assumindo que todos os ângulos estão reduzidos ao primeiro quadrante4.2
| y = cos(arctan(x)) |
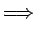 y = y = 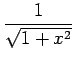 |
|
| y = sin(arctan(x)) |
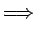 y = y = 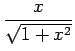 |
(4.1.2) |
| y = sin(arccos(x)) |
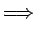 y = y = 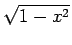 |
|
| y = cos(arcsin(x)) |
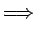 y = y = 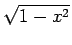 |
|
Aplicando a transformação inversa ao vector
v2 (levando em consideração que
sin(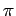 -
- 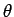 ) = sin(
) = sin(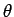 )), tem-se (sublinha-se os termos aos quais uma das fórmulas descritas em 4.1.2 se aplica):
)), tem-se (sublinha-se os termos aos quais uma das fórmulas descritas em 4.1.2 se aplica):
| vx2 |
= vr2cos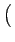 v v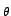 2 2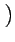 sin sin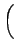 v v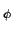 2 2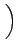 |
|
| |
= vr2 sin sin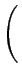  - arcsin - arcsin 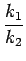 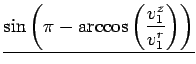   |
|
| |
= 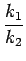 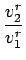 vx1 vx1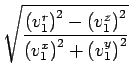 |
|
| |
= 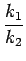 vx1 vx1 |
(4.1.3) |
| vy2 |
= vr2sin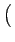 v v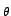 2 2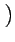 sin sin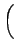 v v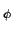 2 2 |
|
| |
= vr2 sin sin  - arcsin - arcsin 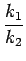 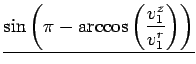   |
|
| |
= 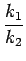 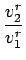 vy1 vy1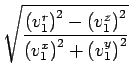 |
|
| |
= 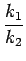 vy1 vy1 |
(4.1.4) |
| vz2 |
= vr2cos v v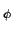 2 2 |
|
| |
= vr2cos  - arcsin - arcsin 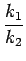 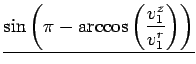   |
|
| |
= - vr2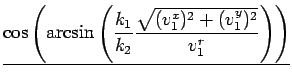 |
|
| |
= - 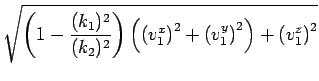 |
|
| |
= - 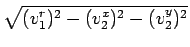 |
(4.1.5) |
Como se evidencia na última expressão, vz2 garante que a norma do vector refractado é igual à do vector incidente. O factor k1/k2 será doravante designado por k. Neste caso em particular, usando uma interface ar/água, ter-se-à
k 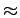 1/1.33.
1/1.33.
Ricardo
2004-11-06
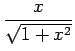
![]() -
- ![]() ) = sin(
) = sin(![]() )), tem-se (sublinha-se os termos aos quais uma das fórmulas descritas em 4.1.2 se aplica):
)), tem-se (sublinha-se os termos aos quais uma das fórmulas descritas em 4.1.2 se aplica):
 sin
sin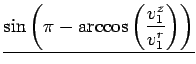
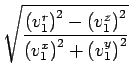
 sin
sin