Calibração das Câmaras e Rectificação de Imagem

Para obter os parâmetros de calibração das câmaras, optou-se por se usar a Camera Calibration Toolbox for Matlab desenvolvida por Jean-Yves Bouguet. Esta toolbox encontra-se disponível na Internet e permite a calibração das câmaras (parâmetros intrínsecos e extrínsecos), usando um alvo semelhante a um tabuleiro de xadrez e baseando-se no trabalho de Zhang [10] e Heikkila [11]. Embora o pacote permita também a rectificação das imagens, desenvolveu-se código em C para este fim, acelerando substancialmente este passo e reduzindo significativamente os requisitos de memória. A calibração permite ainda descrever a posição (e orientação) da câmara face ao alvo, sendo portanto fácil garantir a posição do interface no plano z = 0 e obter os parâmetros extrínsecos da câmara, bastando que uma das imagens de calibração tenha o alvo a flutuar sobre o interface.

Sendo comum a utilização da rectificação convencional (i.e. sem presença de interface), a sua discussão será bastante breve, sendo esta secção dedicada às alterações introduzidas ao processo convencional. Uma descrição formal do processo convencional de rectificação de imagens pode ser encontrado em [10] e [11].

A figura 5.2.1 ilustra os passos necessários à calibração de imagens adquiridas por uma câmara a observar um cenário submerso.

Figura: Diagrama ilustrando os passos necessários à rectificação de uma imagem.

1. Cada pixel da imagem original é primeiro passado para o plano de retina através da matriz 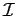$\mathcal {I}$₁^-1 (parâmetros intrínsecos da câmara).

2. Uma vez neste plano é possível compensar o efeito da distorção não linear introduzida pelo sistema de aquisição de imagem. Esta distorção tem normalmente carácter radial, sendo modelizados pelos termos pares de um polinómio em r = 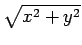$\sqrt{{x^2+y^2}}$ embora efeitos de distorção tangencial sejam também frequentemente compensados.

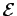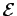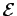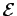3. É então possível aplicar a rectificação dada por uma homografia semelhante a 4.1.9. Infelizmente devido à existência da distorção não linear introduzida pelo sistema ocular das câmaras, não é possível incluir os parâmetros intrínsecos das câmaras na transformação, logo a homografia a aplicar é simplesmente H = $\mathcal {E}$₂M(p₀)$\mathcal {E}$₁^-1, onde $\mathcal {E}$₁ e $\mathcal {E}$₂ são a transformação extrínseca da câmara e a transformação extrínseca desejada para a câmara, respectivamente.

4. Finalmente converte-se o ponto anterior, no plano de água descrito no referencial da câmara alterada, num ponto no plano de retina descrito em pixels através da matriz 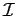$\mathcal {I}$₂ (transformação intrínseca desejada para a câmara). Este passo pode ser combinado com o anterior aumentando a eficiência^5.2.

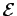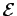A rectificação de forma a ter epipolares horizontais está implícita no passo da transformação de snell, através das matrizes $\mathcal {E}$₁ e $\mathcal {E}$₂. Repare-se que caso não se projectasse sobre o interface e o centro de projecção da câmara não se alterasse ( M(p₀) igual à identidade), o passo 3 seria simplesmente uma rotação, de forma a que os planos de retina de ambas as câmaras se tornassem co-planares. Obviamente que na presença da interface apenas se consegue ``quase-epipolares''.

De forma a garantir que todos os pixels da imagem rectificada tenham um valor de brilho atribuído, todo o processo descrito anteriormente é corrido do fim para o início. Assim, para cada pixel na imagem final, é preciso encontrar o seu correspondente na imagem original. Em cada passo à portanto que aplicar a transformação inversa da que é descrita. O processo de inversão torna o segundo passo mais simples (o processo directo necessita do cálculo de raízes de um polinómio enquanto que a inversa é simplesmente o valor do polinómio), mas o terceiro passo, devido à matriz M( ^. ), não é invertível. Porém, a função ``inversa'' que se procura é simplesmente M(p₁) onde p₁ é o centro de projecção desejado para a nova câmara. Assim, abusando uma vez mais da notação, tem-se que H^-1 = 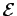$\mathcal {E}$₁M(p₁)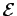$\mathcal {E}$₂^-1.

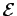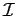Em aberto ficou apenas como obter $\mathcal {E}$₂ e $\mathcal {I}$₂, porém este processo foi já descrito na secção 4.1.3. Exemplos da rectificação de imagens apresentam-se nas figuras 5.2.2 e 5.2.3. Note-se a elevada distorção introduzida pelo sistema ocular das câmaras utilizadas, principalmente no segundo exemplo apresentado onde o baixo zoom torna a lente numa grande angular.

Figura: Em cima as imagens originais, em baixo as mesmas imagens rectificadas. Na figura é visível a mira de calibração usada.

Figura: Em cima as imagens originais, em baixo as mesmas imagens rectificadas. Repare-se na elevada distorção compensada.