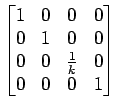Mudança de Parâmetros da Câmara
Assumindo para simplificar um ambiente 2D com p1x = 0 (onde
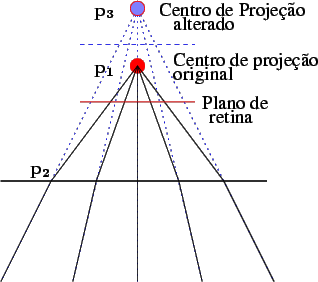
p1 será o centro de projecção da câmara) e que o interface está no plano y = 0 (ver figura 4.1.3), segue-se um raio de luz que parte de
p1, segundo uma direcção
v1. Este atingirá o interface num ponto
p2:
Figura 4.1.3:
Representação do caminho percorrido pela luz quando se usa a aproximação de Snell de primeira ordem.
 |
p2 =
p1 -
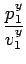 v1
v1
De acordo com a aproximação da lei de Snell de primeira ordem, aí o raio será refractado e continuará o seu percurso segundo uma direcção
v2 = Kv1. Se se propagar este novo raio para trás, e se encontrar o ponto de intersecção com a recta x = 0, tem-se o ponto
p3:
| p3 |
= p2 - 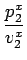 v2 v2 |
|
| |
= p1 - 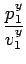 v1 - v1 - 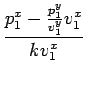 Kv1 Kv1 |
|
| |
= 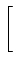 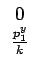 ![$\displaystyle \left.\vphantom{\begin{array}{ccccccc}0\\ \frac{p_1^y}{k}\end{array}}\right]$](img151.gif) |
|
Como se observa,
p3 é independente da direcção tomada inicialmente, descrita por
v1. Generalizando para 3D, para qualquer
p1, tem-se
p3 = 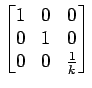 p1 p1 |
(4.1.6) |
Repare-se então que se se alterar o centro de projecção da câmara (originalmente em
p1) para
p3, leva-se em conta o efeito da interface (no sentido da aproximação de Taylor de primeira ordem) e pode-se aplicar directamente a reconstrução tridimensional usual (desde que se considere válida esta aproximação à lei de Snell descrita na secção 4.1.2).
Como se sabe, o centro de projecção de uma câmara está na origem do referencial local à câmara, ou seja:
Sendo
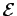 a transformação projectiva que leva pontos do referencial do mundo (W) para o referencial local da câmara (L), tem-se
Como visto na equação 4.1.6 pode-se agora aplicar a aproximação de primeira ordem da lei de snell, resultando em
a transformação projectiva que leva pontos do referencial do mundo (W) para o referencial local da câmara (L), tem-se
Como visto na equação 4.1.6 pode-se agora aplicar a aproximação de primeira ordem da lei de snell, resultando em
onde

=
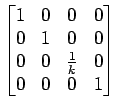
Sendo esta a nova posição da câmara em coordenadas do mundo (parâmetros extrínsecos). A orientação da câmara não necessita de ser alterada neste passo, embora normalmente seja, de forma tornar ambos os planos de retina das câmaras co-planares.
Os parâmetros intrínsecos da câmara, embora também não tenham que ser alterados, normalmente também o são, de forma a aproveitar melhor os elementos de imagem. Caso não se fizesse, apareceria uma zona à volta da imagem sem conteúdo, resultando em percas desnecessárias de informação. A alteração destes parâmetros é porém empírica havendo várias abordagens possíveis, por exemplo manter invariante a área da projecção da imagem no plano de retina ou garantir que dois cantos opostos ao longo de uma diagonal não alterem a sua posição. Dada a sua simplicidade e bons resultados obtidos (levando em conta a natureza da transformação extrínseca que se usa), foi usada esta última.
Ricardo
2004-11-06


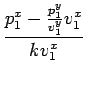 Kv1
Kv1