Estimação do Movimento e Seguimento

Dado um conjunto de pares (xi,yi) para i = [1..N] que se sabe estarem relacionados através de uma transformação linear (contempla-se a possibilidade das medidas estarem afectadas de ruído):

yi $\displaystyle \approx$ Mxi

é possível definir uma medida de erro para cada coordenada de cada par (pontos K-dimensionais), dada por

$\displaystyle \epsilon_{i}^{j}$ = $\displaystyle \sum_{{k=1}}^{K}$mjkxik - yij

onde mjk são as entradas da matriz M nas quais se pretende minimizar. Tentar-se-á minimizar o erro global no sentido de mínimos quadrados:

E = $\displaystyle \sum_{{i=1}}^{{N}}$$\displaystyle \sum_{{j=1}}^{K}$($\displaystyle \epsilon_{i}^{j}$)2

Derivando em ordem a mjk e igualando a 0 (condição necessária de mínimo e suficiente para esta função de custo) resulta em

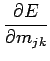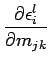$\displaystyle {\frac{{\partial E}}{{\partial m_{jk}}}}$ = $\displaystyle \sum_{{i=1}}^{{N}}$$\displaystyle \sum_{{l=1}}^{K}$2$\displaystyle \epsilon_{i}^{l}$$\displaystyle {\frac{{\partial \epsilon_i^l}}{{\partial m_{jk}}}}$    
  = 2$\displaystyle \sum_{{i=1}}^{{N}}$$\displaystyle \sum_{{n=1}}^{K}$mjnxinxik - yijxik    
  = 0    
$\displaystyle \Longleftrightarrow$ $\displaystyle \sum_{{i=1}}^{{N}}$yijxik = $\displaystyle \sum_{{i=1}}^{{N}}$$\displaystyle \sum_{{n=1}}^{K}$mjnxinxik    $\displaystyle \forall_{{j,k \in [1..K]}}^{}$    
$\displaystyle \Longleftrightarrow$ $\displaystyle \sum_{{i=1}}^{{N}}$yijxik = $\displaystyle \sum_{{n=1}}^{K}$mjn$\displaystyle \sum_{{i=1}}^{{N}}$xinxik    $\displaystyle \forall_{{j,k \in [1..K]}}^{}$    

Que pode ser re-escrito em forma matricial

$\displaystyle \scriptsize \underbrace{\begin{bmatrix} m_{11}& m_{12}&\ldots&m_{... ... y_i^K x_i^2 & \ldots & \sum_{i=1}^{N} y_i^K x_i^K \end{bmatrix}}_{\mathbf{B}} $

Sendo M, a solução que melhor aproxima no sentido do menor erro quadrático a transformação linear desejada, dada por

M = BA-1

Normalmente a transformação linear representará uma rotação seguida de uma translação (transformação rígida) em coordenadas homogéneas e portanto deverá ter a forma

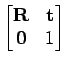
M = $\displaystyle \begin{bmatrix} \mathbf{R} & \mathbf{t}\\ \mathbf{0} & 1 \end{bmatrix}$

onde R $ \in$ SO(3), ou seja pretende-se que M $ \in$ SE(3). Na minimização anterior não se impôs esta restrição (dado o aumento significativo da complexidade de cálculo) e portanto o bloco de M correspondente à matriz de rotação deverá ser projectado em SO(3). A melhor projecção (uma vez mais no sentido de menor erro quadrático) é dada pela solução do problema de Procrustes (ver [15]). Assim, a solução do problema

W* = arg$\displaystyle \underset{\mathbf{W}}{\textrm{min}}$$\displaystyle \left\Vert\vphantom{ \mathbf{R}-\mathbf{W}}\right.$R - W$\displaystyle \left.\vphantom{ \mathbf{R}-\mathbf{W}}\right\Vert_{F}^{2}$
s.t.WTW = I
 (5.5.1)

pode ser obtida através de uma decomposição SVD. Se R = U$ \Sigma$VT for a decomposição SVD de R, a solução de 5.5.1 vem dada por

W* = UVT

e é única caso $ \Sigma$ tenha rank completo.5.6

Os pares de pontos iniciais podem ser obtidos através de um algoritmo semelhante ao descrito na secção 5.3.1. O seguimento multi-objecto é conseguido através de uma implementação do algoritmo RANSAC (Random Sample Consensus, ver [18]).

Infelizmente o facto de só se obter imagens antes e depois de se alterar o cenário, complica conseguir-se o emparelhamento de características dado que muitas regiões aparecem ocludidas ou simplesmente mudam tão significativamente de pose que são irreconhecíveis. Assim, não é viável usar este método, sendo necessário um outro método que não seja baseado em características.

Outra abordagem possível ao problema de seguimento consiste em observar os deslocamentos volumétricos a partir da reconstrução do cenário antes e depois de ter havido deslocamento. Se se subtrair os dois mapas observam-se regiões positivas (uma pedra deslocou-se para a região) e regiões negativas (uma pedra saiu da região). Esta subtracção tem que ser feita com cuidado dado que os pontos de amostragem são diferentes onde houve deslocamento. Desta forma calcula-se o volume de cada região em cada reconstução, subtraindo-se de seguida os volumes de regiões correspondentes. Nas regiões onde não ocorreu movimento, não havendo movimento das câmaras, os pontos de amostragem são os mesmos nas duas reconstruções tornando este resultado válido. É possível ainda usar a variação de intensidade ou correlação para ajudar na detecção de regiões onde ocorre movimento (técnica usual em 2D).

A solução adoptada para tentar resolver o problema do seguimento consiste em aplicar o algoritmo do simplex a um funcional de custo que tente emparelhar volumes de saída com volumes de chegada, levando em consideração custos de potencial (uma pedra mais facilmente terá tendência a descer que a subir) e distância percorrida. Na figura 5.5.1 apresenta-se os resultados obtidos quando aplicado a um cenário onde apenas 1 elemento do molhe se mexeu (os elementos à volta porém sofreram também ligeiras perturbações).

Figura: Estimação de movimento usando apenas informação de deslocamento volúmico. Em cima: Imagens antes e depois (a claro indica-se as regiões onde se detectou movimento e une-se as regiões emparelhadas), em baixo: regiões de movimento e respectivo volume de cada.
\includegraphics[width=200pt]{movement_mask_before.eps}
\includegraphics[width=200pt]{movement_mask_after.eps}
\includegraphics[width=200pt]{movement_mask.eps}
Região
1 0.0028
2 0.1221
3 0.0008
4 -0.0000
5 -0.0018
6 -0.0006
7 -0.0010
8 -0.0002
9 -0.2284

Dada a forma irregular dos elementos constituintes do molhe (tetrápodes), o uso de volumes fica consideravelmente prejudicado dado que o volume útil (observado) ocupado por cada depende da maneira como este encaixou nos restantes. Como se observa na tabela incluída na figura 5.5.1, um dado tetrápode ocupa volumes bastante diferentes consoante a sua posição (comparar região 2 e 9, correspondentes às regiões de partida e de chegada do tetrápode).

Ricardo 2004-11-06