Emparelhamento Esparso
O algoritmo implementado, descrito em [12] faz uso de correlação entre características para calcular a matriz de permutação que maximiza o ganho global do problema. Se se empilhar os valores de intensidade dos pixels de janelas de tamanho NxN centradas nas características encontradas, nas linhas de duas matrizes
F1 e
F2 (imagem 1 e 2, respectivamente), a correlação entre todas estas obtém-se fazendo
C = F1F2T. O problema da correspondência resume-se então a encontrar uma matriz de permutação parcial
P que resolva o seguinte problema de maximização:
P* = arg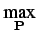 | trace(PF1F2T) |
| s.t. | P 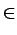 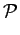 P(p1, p2) P(p1, p2) |
|
(5.3.1) |
onde
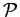 P(p1, p2) designa o conjunto de matrizes de permutações parciais de tamanho p1xp2 (número total de características na imagem 1 e 2 respectivamente). Uma matriz de permutação parcial é uma matriz de permutação que permite que algumas das suas linhas e colunas sejam zero. De forma a evitar muitas falsas correspondências, impõe-se que a matriz de permutações parciais tenha rank k (ou seja, serão gerados apenas os k emparelhamentos mais fortes), por exemplo
k = min(p1, p2)/2.
P(p1, p2) designa o conjunto de matrizes de permutações parciais de tamanho p1xp2 (número total de características na imagem 1 e 2 respectivamente). Uma matriz de permutação parcial é uma matriz de permutação que permite que algumas das suas linhas e colunas sejam zero. De forma a evitar muitas falsas correspondências, impõe-se que a matriz de permutações parciais tenha rank k (ou seja, serão gerados apenas os k emparelhamentos mais fortes), por exemplo
k = min(p1, p2)/2.
A imposição de algumas outras restrições é possível através de uma matriz
S (designada matriz de suporte) que indica quais os emparelhamentos que são possíveis à partida. Assim é possível rejeitar correspondências que nunca poderão fazer parte da solução global, diminuindo significativamente o espaço de procura. Em particular se as imagens tiverem sido previamente rectificadas, características em linhas diferentes (ou a um dado número de linhas de distância) nunca deverão ser emparelhadas.
As características escolhidas para este problema são cantos, fazendo uso do detector de cantos de Harris. Julga-se que para o ambiente em questão (um monte de pedras com cantos bem definidos), o seu uso é apropriado. O problema linear 5.3.1 é resolvido usando o método do simplex e foi usada uma implementação deste criada por Michel Berkelaar (lp_solve). Ver figura 5.3.1 para um exemplo de resultados obtidos.
Figura 5.3.1:
À esquerda: imagem esquerda previamente rectificada. À direita: reconstrução tridimensional do modelo usando uma grelha de triângulos. Foi usado stereo esparso como descrito em [12]. As unidades dos eixos são pixels (espaço de disparidade) e a orientação do modelo foi escolhida de forma a melhor o ilustrar.
![\includegraphics[width=200pt]{left_color_calib.eps}](img270.gif)
![\includegraphics[width=200pt]{disparity_maciel.eps}](img277.gif) |
Embora o algoritmo produza bons resultados, a necessidade de emparelhamento denso para o algoritmo de estimação da interface limita a utilidade deste. O algoritmo foi porém usado numa tentativa de seguimento das peças constituintes do molhe.
Ricardo
2004-11-06
![\includegraphics[width=200pt]{left_color_calib.eps}](img270.gif)
![\includegraphics[width=200pt]{disparity_maciel.eps}](img277.gif)