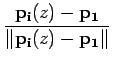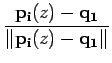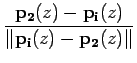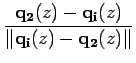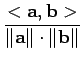Supondo que se tem duas câmaras (centro de projecção em
p1 e
q1) e duas imagens das quais se conhece a correspondência de cada pixel com um ponto submerso.4.6 Fixando um par
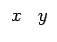
![$ \left.\vphantom{\begin{array}{ccccccc}x & y\end{array}}\right]$](img239.gif) e fazendo variar z, pode-se definir a função
pi(z) =
e fazendo variar z, pode-se definir a função
pi(z) = 
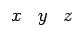
![$ \left.\vphantom{\begin{array}{ccccccc}x & y &z\end{array}}\right]^{T}_{}$](img242.gif) e os versores
e os versores
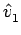 (z) e
(z) e
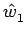 (z) (que unem o ponto
p1 ao ponto
pi(z) e o ponto
q1 ao ponto
pi(z), respectivamente como representado na figura 4.2.3):
(z) (que unem o ponto
p1 ao ponto
pi(z) e o ponto
q1 ao ponto
pi(z), respectivamente como representado na figura 4.2.3):
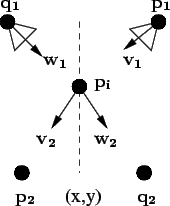
Figura:
Estimação do interface fixando duas coordenadas.
 |
Como se supõe que se conhece a correspondência de cada pixel em cada imagem a um ponto submerso,
p2 e
q2 (pontos submersos correspondentes aos pares
(p1, 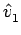 ) e
(q1,
) e
(q1, 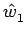 ), respectivamente) são também funções de z. Assim são também funções de z os versores que unem
pi a
p2 e
q2:
), respectivamente) são também funções de z. Assim são também funções de z os versores que unem
pi a
p2 e
q2:
usando a equação 4.2.3 obtêm-se duas orientações possíveis para o interface (
up e
uq), uma para cada imagem, ambas em função de z. O objectivo é encontrar z para o qual as duas orientações sejam iguais. Dado que apenas se dispõe de um conjunto discreto de z possíveis (dada a natureza discreta das imagens) pode-se usar técnicas de interpolação e de regressão de forma a minimizar o ruído. O problema pode ainda ser formulado como um problema de optimização:
onde
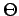 ( . , . ) devolve o ângulo entre os dois vectores que aceita como argumentos, ou seja
Em particular, sabe-se que o mínimo global (do problema não discretizado) tem custo nulo. Repetindo o método anterior para uma grelha de pontos x e y, obtém-se uma amostragem da superfície do interface.
( . , . ) devolve o ângulo entre os dois vectores que aceita como argumentos, ou seja
Em particular, sabe-se que o mínimo global (do problema não discretizado) tem custo nulo. Repetindo o método anterior para uma grelha de pontos x e y, obtém-se uma amostragem da superfície do interface.
É ainda possível encontrar uma solução global construindo um volume de erros
e(x, y, z) =
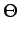
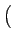 up(x, y)
up(x, y)(
z),
uq(x, y)(
z)
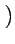
e aplicar um algoritmo de programação dinâmica a dois passos como descrito em [9], de forma a encontrar a superfície z = S(x, y) neste espaço tridimensional que minimize, por exemplo,
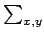
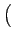 e(x, y, S(x, y))
e(x, y, S(x, y))
Ricardo
2004-11-06