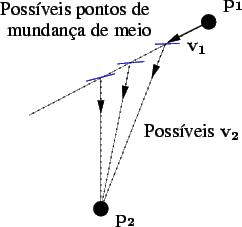
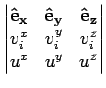Pretende-se nesta secção estimar a superfcie da interface, onde se assume que a superfície é função de x e y. Como se observa na figura 4.2.1, mesmo que se tenha disponível a correspondência de pontos na câmara (fixando
v1) com pontos
p2 no cenário, não é possivel obter os parâmetros que definem a interface, existindo ainda um grau de liberdade. Só usando a informação existente na segunda câmara se torna possivel obter a localização e orientação da interface.
Figura:
Representação gráfica de possíveis pontos de transição de meio. Como representado, em cada um destes pontos o plano tangente ao interface terá uma orientação diferente.
 |
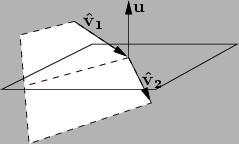
A lei de Snell pode ser escrita em formato vectorial como ilustra a figura 4.2.2 [8]
Figura:
Lei de Snell a 3 dimensões. Note-se que a lei de snell para 2D é valida se se considerar apenas o plano sombreado.
 |
onde
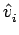 designa a direcção do raio de luz no ambiente i, e
designa a direcção do raio de luz no ambiente i, e
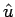 designa a normal à interface. Note-se que para a equação ser válida, os
designa a normal à interface. Note-se que para a equação ser válida, os
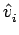 têm necessariamente que ter norma igual (em particular, força-se que a norma seja unitária), enquanto que a norma de
têm necessariamente que ter norma igual (em particular, força-se que a norma seja unitária), enquanto que a norma de
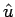 não é importante, perdendo o atributo de versor e passando a ser designado por
u. Expandindo o produto externo:
não é importante, perdendo o atributo de versor e passando a ser designado por
u. Expandindo o produto externo:
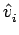 x u x u |
= |
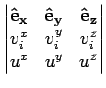 |
|
| |
= |
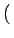 viyuz - vizuy viyuz - vizuy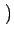 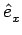 + + 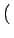 vizux - vixuz vizux - vixuz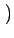 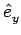 + + 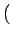 vixuy - viyux vixuy - viyux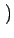 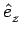 |
|
onde
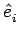 ,
i
,
i 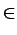 {x, y, z}, designam os versores de base. Portanto, a lei de Snell impõe:
{x, y, z}, designam os versores de base. Portanto, a lei de Snell impõe:
k1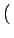 v1yuz - v1zuy v1yuz - v1zuy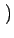 |
= k2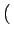 v2yuz - v2zuy v2yuz - v2zuy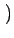 |
|
k1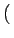 v1zux - v1xuz v1zux - v1xuz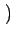 |
= k2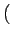 v2zux - v2xuz v2zux - v2xuz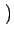 |
(4.2.1) |
k1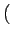 v1xuy - v1yux v1xuy - v1yux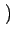 |
= k2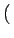 v2xuy - v2yux v2xuy - v2yux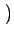 |
|
Repare-se que as equações 4.1.3 a 4.1.5 poderiam ter sido obtidas daqui, fazendo
u = 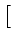
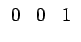
![$ \left.\vphantom{\begin{array}{ccccccc}0 & 0 & 1\end{array}}\right]^{T}_{}$](img231.gif) e forçando
e forçando
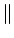 v2
v2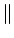 = 1. Tomando
= 1. Tomando
| ix |
= |
k1v1x - k2v2x |
(4.2.2) |
| iy |
= |
k1v1y - k2v2y |
(4.2.3) |
| iz |
= |
k1v1z - k2v2z |
(4.2.4) |
pode-se reescrever 4.2.1 como
| iyuz |
= |
izuy |
|
| izux |
= |
ixuz |
|
| ixuy |
= |
iyux |
|
Como se afirma que a norma de
u não é importante, o sistema anterior é sub-especificado, sendo a solução dada à parte de um factor de escala. Uma solução possível é então:
Infelizmente
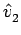 não é conhecido à partida. Porém, se se admitir que se conhece o ambiente submerso e que se tem o problema do emparelhamento resolvido, conhecem-se
p1 (centro de projecção da câmara no ambiente 1),
p2 (dado pela reconstrução do ambiente 2) e
não é conhecido à partida. Porém, se se admitir que se conhece o ambiente submerso e que se tem o problema do emparelhamento resolvido, conhecem-se
p1 (centro de projecção da câmara no ambiente 1),
p2 (dado pela reconstrução do ambiente 2) e
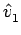 (direcção tomada por um raio de luz para ir de
p1 a
p2 sofrendo a acção da interface), pode-se tentar resolver o problema por duas abordagens distintas. A primeira é semelhante a uma transformada de Hough enquanto que a segunda consiste em fixar duas coordenadas (x e y) e variar z até se ter uma solução consistente.
(direcção tomada por um raio de luz para ir de
p1 a
p2 sofrendo a acção da interface), pode-se tentar resolver o problema por duas abordagens distintas. A primeira é semelhante a uma transformada de Hough enquanto que a segunda consiste em fixar duas coordenadas (x e y) e variar z até se ter uma solução consistente.
Subsecções
Ricardo
2004-11-06