Dado que a luz se propaga em linha recta em cada meio, pode escrever-se (ver figura 4.2.1):
p2 =
p1 +
t1
+
t2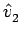
ou seja
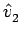 = = 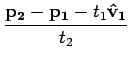 |
(4.2.6) |
como a norma de
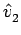 terá que ser unitária, o valor de t2 vem necessariamente dado por
Obtêm-se assim valores possíveis para
terá que ser unitária, o valor de t2 vem necessariamente dado por
Obtêm-se assim valores possíveis para
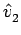 parametrizados por t1, e portanto
u fica também parametrizado por esta variável. Então, t1 parametriza tanto a localização do ponto de intersecção do raio que parte de
p1 segundo a direcção
parametrizados por t1, e portanto
u fica também parametrizado por esta variável. Então, t1 parametriza tanto a localização do ponto de intersecção do raio que parte de
p1 segundo a direcção
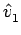 com a interface4.4, como a orientação da interface nesse mesmo ponto4.5. Se se levar em consideração que se tem 2 imagens (cada uma com MxN diferentes
com a interface4.4, como a orientação da interface nesse mesmo ponto4.5. Se se levar em consideração que se tem 2 imagens (cada uma com MxN diferentes
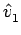 ) deverá ser possível encontrar a superfície da interface usando técnicas semelhantes à transformada de Hough (infelizmente num espaço a 5 dimensões, com coordenadas
(x, y, z, vx, vy) dado que vz fica definido das duas últimas).
) deverá ser possível encontrar a superfície da interface usando técnicas semelhantes à transformada de Hough (infelizmente num espaço a 5 dimensões, com coordenadas
(x, y, z, vx, vy) dado que vz fica definido das duas últimas).
Devido às dimensões do espaço de procura, este método requer uma implementação cuidada de forma a manter uma baixa utilização de memória. Dada esta dificuldade considera-se a abordagem descrita de seguida como sendo melhor.
Ricardo
2004-11-06