As equações que levam um ponto no plano de retina (que pode ser pensado como o plano z = 1 em coordenadas locais à câmara) para coordenadas de imagem são dadas por [4]
| u |
= fxx + cx |
|
| v |
= fyy + cy |
|
onde se ignora a distorção introduzida pelo sistema de aquisição de imagem, supondo portanto que estas foram previamente corrigidas neste sentido. Caso o ponto não esteja no plano z = 1 há primeiro que o projectar sobre este plano, passando o anterior a ser escrito como
| u |
= fx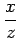 + cx + cx |
|
| v |
= fy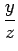 + cy + cy |
|
Este último sistema pode ser escrito como uma transformação projectiva, assumindo a forma
Podemos ainda pensar na transformação ``inversa'' que converte um valor descrito em coordenadas de imagem, no seu correspondente no plano de retina em z = 1:
| x |
= 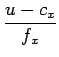 |
|
| y |
= 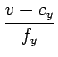 |
|
| z |
= 1 |
|
ou seja,
Repare-se que se abusa da notação ao escrever
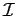 -1 dado que
-1 dado que
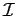 não é invertível. Pode-se então também pensar na transformação que leva um ponto descrito em coordenadas do mundo em coordenadas de imagem
não é invertível. Pode-se então também pensar na transformação que leva um ponto descrito em coordenadas do mundo em coordenadas de imagem
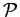 =
= 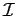
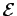 onde
onde
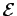
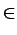 SE(3)3.1 é a transformação de coordenadas do referencial do mundo para o referencial da câmara (que designaremos por parâmetros extrínsecos da câmara). À matriz
SE(3)3.1 é a transformação de coordenadas do referencial do mundo para o referencial da câmara (que designaremos por parâmetros extrínsecos da câmara). À matriz
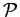 designaremos de matriz de projecção da câmara. Usando o conceito descrito anteriormente é também possível descrever um pixel como um ponto no plano de retina em coordenadas do mundo usando a transformação
designaremos de matriz de projecção da câmara. Usando o conceito descrito anteriormente é também possível descrever um pixel como um ponto no plano de retina em coordenadas do mundo usando a transformação
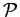 -1 =
-1 = 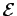 -1
-1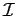 -1. Tal como na escrita de
-1. Tal como na escrita de
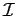 -1, abusa-se uma vez mais da notação dado que
-1, abusa-se uma vez mais da notação dado que
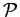 -1
-1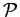
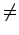 I embora
I embora
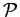
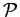 -1 = I (onde
I é a identidade).
-1 = I (onde
I é a identidade).
Os parâmetros extrínsecos das câmaras são representados (por uma questão de escrita compacta) através de dois triplos em
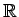 3, um dos quais representa um eixo de rotação passando pela origem do referencial e cuja amplitude descreve o ângulo de rotação, e um segundo triplo em
3, um dos quais representa um eixo de rotação passando pela origem do referencial e cuja amplitude descreve o ângulo de rotação, e um segundo triplo em
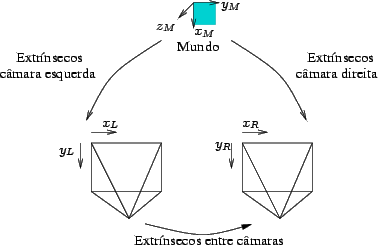
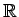 3 descrevendo uma translação a ser aplicada após a rotação. Estes 6 parâmetros são facilmente convertidos em matrizes de transformação de referenciais (e vice-versa) usando a fórmula de Rodrigues [5]. Observe-se a figura 3.3.1 para uma representação dos sistemas de coordenadas usados.
3 descrevendo uma translação a ser aplicada após a rotação. Estes 6 parâmetros são facilmente convertidos em matrizes de transformação de referenciais (e vice-versa) usando a fórmula de Rodrigues [5]. Observe-se a figura 3.3.1 para uma representação dos sistemas de coordenadas usados.
Figura 3.3.1:
Representação dos sistemas de coordenadas usados. A azul representa-se a posição usual do plano de água em z = 0.
 |
Ricardo
2004-11-06
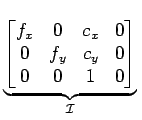
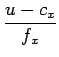
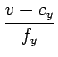
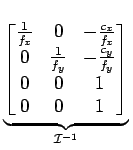
![]() 3, um dos quais representa um eixo de rotação passando pela origem do referencial e cuja amplitude descreve o ângulo de rotação, e um segundo triplo em
3, um dos quais representa um eixo de rotação passando pela origem do referencial e cuja amplitude descreve o ângulo de rotação, e um segundo triplo em
![]() 3 descrevendo uma translação a ser aplicada após a rotação. Estes 6 parâmetros são facilmente convertidos em matrizes de transformação de referenciais (e vice-versa) usando a fórmula de Rodrigues [5]. Observe-se a figura 3.3.1 para uma representação dos sistemas de coordenadas usados.
3 descrevendo uma translação a ser aplicada após a rotação. Estes 6 parâmetros são facilmente convertidos em matrizes de transformação de referenciais (e vice-versa) usando a fórmula de Rodrigues [5]. Observe-se a figura 3.3.1 para uma representação dos sistemas de coordenadas usados.
