Supondo que se pretende minimizar o erro quadrático da regressão, pode-se definir uma medida de erro
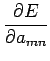 = 2 = 2 |
|
Definindo então N2 equações lineares com N2 variáveis, que
podem ser reescritas em forma matricial, onde para abreviar se usa
a notação
( . ) ![]()
![]() ( . ) e
Pij
( . ) e
Pij ![]() Pij(Xl, Yl):
Pij(Xl, Yl):
A solução procurada é então obtida através de x = A-1b. De notar porém que o sistema é muito mal condicionado numericamente como se descreve de seguida. Suponha-se que se pretende calcular um polinómio de ordem 5 que melhor se ajuste a dados que apresentem uma variação de 10n unidades em cada variável. Se se usar a base de polinómios ``convencional'' ( Pij(X, Y) = XiYj) a diferença de ordem das entradas da última linha da matriz face à primeira seria da ordem de 1010n, tornando as linhas quase linearmente dependentes devido a problemas de precisão finita. De forma a aliviar este problema (ver [16]), escolhe-se uma base de polinómios ortogonal num intervalo de -1 a 1 (em particular escolhem-se polinómios de Legendre), ou seja:
Repare-se que se pode usar a base de polinómios de uma variável para construir os polinómios bivariados, ou seja Pij(X, Y) = Pi(X)Pj(Y). É fácil demonstrar que a construção resulta em polinómios ortogonais:
| = |
||
| = |
||
| = cj |
||
| = cicj |
Alternativamente, os polinómios ortogonais (univariados ou bivariados) podem ser construídos através do processo de ortogonalização de Gram-Schmidt aplicado à base já previamente designada por ``convencional''. Apresenta-se de seguida a base ortogonal de polinómios univariados usada (Legendre):
| P0(X) | = 1 | |
| P1(X) | = X | |
| P2(X) | = |
|
| P3(X) | = |
|
| P4(X) | = |
|
| P5(X) | = |
|
| P6(X) | = |
|
| P7(X) | = |
|
| P8(X) | = |
|
| P9(X) | = |
Repare-se porém que a base é ortogonal apenas no intervalo
X ![]() [- 1..1] portanto exige um pré-escalamento dos dados de
entrada a este intervalo. No caso de polinómios bivariados o mesmo
se aplica às duas variáveis. Repare-se que se os dados estiverem
espalhados uniformemente neste intervalo, a condição
A.1 é aproximada (tanto melhor quanto mais
densos forem os dados), tornando a matriz
A
praticamente diagonal. Assim, a complexidade de computação diminui
substancialmente, sendo a inversão da matriz de tamanho
(N + 1) x (N + 1) reduzida a N + 1 divisões.
[- 1..1] portanto exige um pré-escalamento dos dados de
entrada a este intervalo. No caso de polinómios bivariados o mesmo
se aplica às duas variáveis. Repare-se que se os dados estiverem
espalhados uniformemente neste intervalo, a condição
A.1 é aproximada (tanto melhor quanto mais
densos forem os dados), tornando a matriz
A
praticamente diagonal. Assim, a complexidade de computação diminui
substancialmente, sendo a inversão da matriz de tamanho
(N + 1) x (N + 1) reduzida a N + 1 divisões.
Uma particularidade adicional do uso de polinómios ortogonais sobre dados uniformemente distribuídos no intervalo [- 1..1] x [- 1..1] é que a solução para uma regressão de certa ordem inclui toda a informação para regressões de ordem inferior. Em particular, se