06.25
Update: you can check some photos of the workshop here.
Update: you can check some photos of the workshop here.
Together with João Fayad and Lourdes Agapito we are trying to deal with the problem of reconstructing complex non-rigid objects. A face deforming can be approximated easily by a set of linear 3D model but, for instance, a flag waving in the wind is a different matter. For such problem, we are presenting a new framework for dealing with such complex shapes based on piecewise quadratic approximations of the deforming body. This video shows 3D modelling results from 2D images for two highly non-linear deformations:
These three slides schematically resumes the pipeline used for the 3D reconstruction:

Pipeline for Piecewise Reconstruction Step 1-2

Pipeline for Piecewise Reconstruction Step 3-4
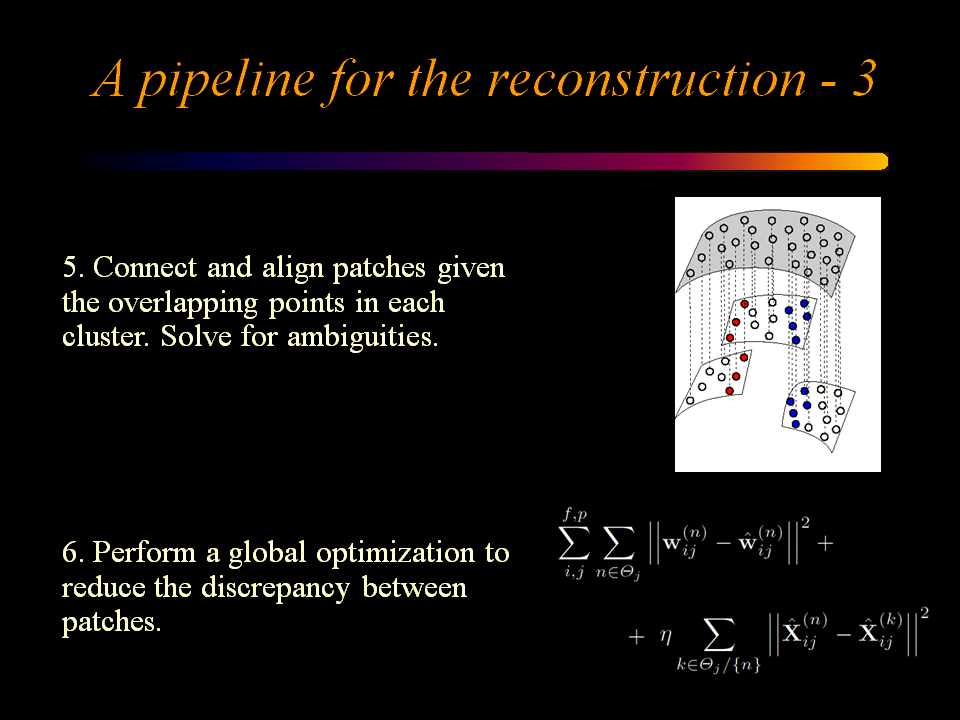
Pipeline for Piecewise Reconstruction Step 5-6
This work will be presented this year in ECCV 2010. More information and the paper will appear soon in these pages.
@inproceedings{Fayad:etal:2010,
author = {J. Fayad and L. Agapito and A. {Del Bue}},
title = {Piecewise Quadratic Reconstruction of Non-Rigid Surfaces from Monocular Sequences},
editor = {Kostas Daniilidis and Petros Maragos and Nikos Paragios},
booktitle = {Computer Vision -- ECCV 2010},
publisher = {Springer},
location = {Heidelberg},
series = {Lecture Notes in Computer Science},
volume = {6314},
year = {2010},
isbn = {978-3-642-15560-4},
pages = {297--310}
}
We are presenting the BALM — a general computational framework for optimising various bilinear problems! We hope this algorithm will ease the life of many researchers when optimising several classes of bilinear problems such as rigid and non-rigid structure from motion, photometric stereo, image registration, learning by factorization and many more. The computational core is based on Augmented Lagrange Multipliers method and the main feature is that it can deal with specific manifold constraints on one of the bilinear component. This is the problem we optimise:
where is a matrix containing our measured data (e.g. image point trajectories in SfM or image pixels variations for Photometric Stereo). The matrices
and
represents our bilinear components to estimate. The matrix
is formed as:
Each of the sub-matrices lies on a specific manifold
(i.e. its values are not arbitrary but constrained). When dealing with SfM the manifolds are usually Stiefel while with Photometric Stereo are mostly spherical.
Now a video showing the resilience of BALM to missing data in structure from motion and photometric stereo problems:
At the moment we have found more then 12 problems that can be explained with bilinear models and thus solved with BALM. Some examples: 2D-3D registration of rigid/articulated/non-rigid models, Structure from Sound, BRDFs factorisation for Computer Graphics, Modelling pose/expression/identity, gait analysis and many more. More details and the code will appear soon in a dedicated research area.
Update: check the paper pdf here
@inproceedings{DelBue:etal:2010,
author = {A. {Del Bue} and J. Xavier and L. Agapito and M. Paladini},
title = {Bilinear Factorization via Augmented Lagrange Multipliers},
editor = {Kostas Daniilidis and Petros Maragos and Nikos Paragios},
booktitle = {11th European Conference on Computer Vision (ECCV 2010), Crete, Greece},
publisher = {Springer},
location = {Heidelberg},
series = {Lecture Notes in Computer Science},
volume = {6314},
year = {2010},
isbn = {978-3-642-15560-4},
pages = {283--296}
}
I am currently collaborating with my former colleagues in Lisbon in the PrintART project. The aim is to provide image analysis and learning tools to aid the study of paintings and Portuguese tile art. Check this brief description of the project, I hope you will find it interesting:
 |
This is a project that gathers researchers from ISR/IST, the Faculdade de Letras da Universidade de Lisboa, and the Museu Nacional do Azulejo with the purpose of designing a software to aid the study and the identification of Portuguese tile art. The project aims to develop a tool that enables the cross-reference of information, matching prints and tiles, so as to identify the original sources of any given panel, as well as matching the tile panels and the figures portrayed in them. |
Good news! I have three papers in ECCV this year In the next weeks I will show some previews and videos about the new stuff.
 Here in Italy I have met together with an old friend of mine, Carlo, and we had a chat on computer vision and next generation computer games. Some beers were involved as well and everything was framed into a podcast by Carlo. You can listen it here in Tecnica Arcana (sorry, only in Italian).
Here in Italy I have met together with an old friend of mine, Carlo, and we had a chat on computer vision and next generation computer games. Some beers were involved as well and everything was framed into a podcast by Carlo. You can listen it here in Tecnica Arcana (sorry, only in Italian).
I have moved back to Italy. I am now Senior PostDoc at the Computer Imaging facility of the Italian Institute of Technology.
A new addition to the Code page. You can find a set of MATLAB functions for the registration of deformable 3D models given a set of 2D image points. The complete description of this algorithm is available in the paper recently presented at ICIP 2009:
@conference{DelBue:2009, title={2D-3D Registration Of Deformable Shapes With Manifold Projection},
author={A. {Del Bue} and M. Stosic and M. Dodig and J. Xavier},
booktitle = "International Conference on Image Processing (ICIP 2009), Cairo, Egypt", year={2009}
}
A brief description can be found in a previous post on the subject
@conference{DelBue:2009, title={2D-3D Registration Of Deformable Shapes With Manifold Projection},
author={A. {Del Bue} and M. Stosic and M. Dodig and J. Xavier},
booktitle = "International Conference on Image Processing (ICIP 2009), Cairo, Egypt", year={2009}
}
We have released a new MATLAB toolbox for non-rigid and articulated Structure from Motion:
http://www.dcs.qmul.ac.uk/~lourdes/code
The code is available for download and it is the result of our most recent work in collaboration with Marco Paladini, João Xavier, Lourdes Agapito, Marko Stošić and Marija Dodig. If it is used for comparison purposes with other NRSfM methods please cite our CVPR paper:
@conference{paladini:etal:2009, title={{Factorization for Non-Rigid and Articulated Structure using Metric Projections}},
author={M. Paladini and A. {Del Bue} and M. Sto{\v{s}}ic and M. Dodig and J. Xavier and L. Agapito},
year={2009},
pages={2898--2905},
booktitle={Proc. IEEE Conference on Computer Vision and Pattern Recognition, Miami, Florida}
}
Addtional information can be found in the CODE page.