Linear and Nonlinear State-Space Control Theory
Using
Matlab to explore more the practice-class problems
Josť Gaspar
The default location for this webpage is http://www.isr.tecnico.ulisboa.pt/~jag/course_utils/cee/
The problems here referred are from the collection made by Professor Jo„o Miranda Lemos
Note1: This page is not the solution
of the exercises (yes, you still need to attend the practice-classes of the
course). This page is in essence a collection of extra information or
simulations obtained / helped by the use of Matlab.
Notes2: The control toolbox is necessary for most of the examples shown bellow.
In order to overview the control toolbox just type in the Matlab prompt the command doc control
P1. Simulation of a two capacitors circuit using the state space model.
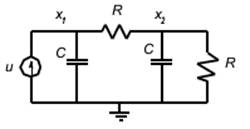
In these simulations R=1KOhm and
C=1mF. Alternative models are generated using random changes of basis. Download
the simulation files p1.m and p1b.m.
To run the simulation files open the files with Matlab
and press F5 or type their names in the command line (assuming you are in the
right folder).
P2. Mass-spring-damper
system
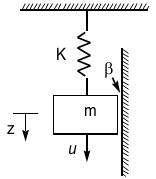
Phase portrait, initial guesses
using just the dynamics matrix: download p2c.mdl, p2c_tst0.m and p2c_tst1.m
. For a partial demo run tst0. Run tst1 for the complete demo. These demos
require also Simulink.
P4.
Conversion between models: transfer function to state-space. In Matlab (control toolbox) you can do simply [A,B,C,D] = tf2ss(num, den)
Challenge: write your own Matlab function that converts a transfer function to a
state space model. Conversion in the simplest case where the degree of the
numerator is lower than the degree of the denominator can be seen in my_tf2ss.m and tested by running that function
without arguments.
P5. Mass-Spring-Dumper time response. To see phase space
drawings run p5b.m, where two cases are considered,
namely having or not having damping.
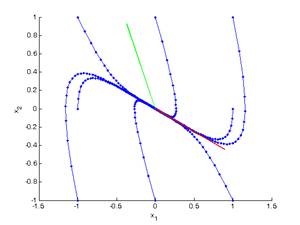
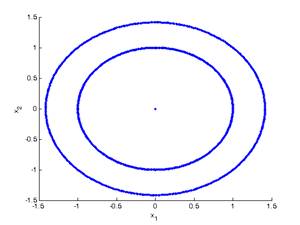
P6.
Obtaining transition matrices for systems can be based in the inverse ![]()
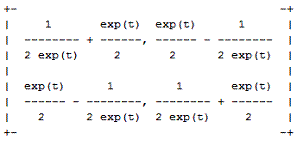
P11. The two
populations cannot coexist. See p11_tst.m
and p11_sh_np.m. Depending on the initial
conditions, one of the populations is going to disappear. In the next table (N0,P0)
denote equilibrium points:
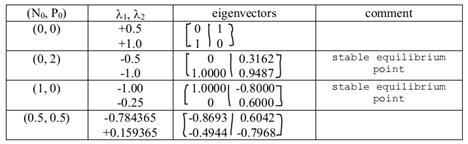
Notice that stable points are (0,2)
and (1,0), so there is no option of (a,b) with a and
b simultaneously not zero.
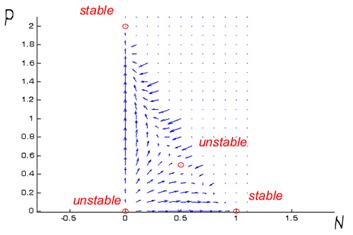
Graphically, local directions show
convergence towards the extinction of one or the other population:
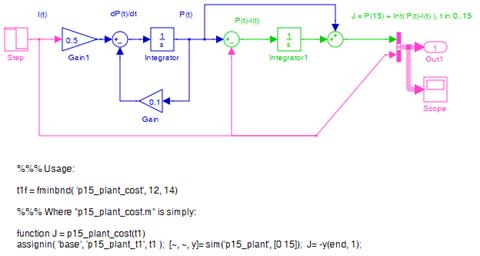
P15. The
investment problem shows that maximizing the profit at year 15 implies stopping
the investment at year 13.82 (considering all years have the same length, .82
means 82% of the length of one year). Download p15_plant.mdl,
p15_plant_cost.m and p15_plant_tst.m,
and run p15_plant_tst. The simulink file is the
following (notice the integrator, in green, to make the merit function J).
The optimal case is the following:
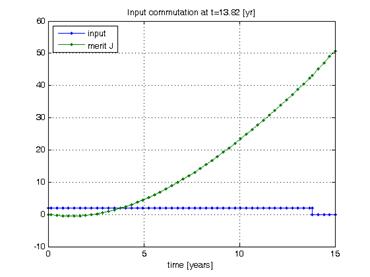
Notice that the investment ends before
year 15 (the horizontal scale is correct; dots do not correspond to years).
P16. Minimizing a cost function, based in a LTI
system, quadratic in the output and control signals, using Chang-Letov's theorem is a particular case of a Linear Quadratic
Regulator (LQR) problem.
Given the system:
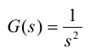
which can be represented as a two
dimensions state space, and given the cost:
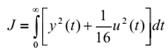
one can rewrite the cost
minimization problem in order of the input u(t)
and as a function of the state x(t).
Expanding the output y(t) as a linear
combination of the state, y(t)=Cx(t) allows obtaining an expression for the squared
output:
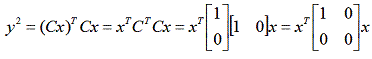
and therefore one obtains the LQR:

which is solved by finding the gains
vector K of the full state linear
feedback u(t)=-Kx(t).
In Matlab
everything is now a couple of instructions:
A= [0 1; 0 0]; B= [0 1]'; C= [1 0];
Q= C'*C; R= 1/16;
K= lqr(A, B, Q, R)
Note that the closed loop solution
is stable due to the design process. See p16_tst.m.