-
A. Del Bue and A. Bartoli, "Multiview 3D Warps," in 13th Internationl Conference on Computer Vision (ICCV 2011), Barcelona, Spain, 2011.
@inproceedings{DelBue:Bartoli:2011,
author = {A. {Del Bue} and A. Bartoli},
title = {Multiview 3D Warps},
booktitle = {13th Internationl Conference on Computer Vision (ICCV 2011), Barcelona, Spain},
year = {2011},
month = {November}
}
Introduction
M3DW is a 3D dense modelling approach using single images that bridges classical image warping methods and the Non-rigid Structure from Motion (NRSfM) framework. M3DW combine the advantages of both; they have an explicit 3D component and a set of 3D deformations combined with projection to 2D. They thus capture the dense deforming body’s time-varying shape and camera pose. The advantages over the classical solutions are numerous: thanks to our feature-based estimation method for the multiview 3D warps, one can not only augment the original images but also retarget or clone the observed body’s 3D deformations by changing the pose.
Method Description
Our algorithm uses as an input a set of 2D image trajectory extracted from a video sequence showing a deforming body:
M3DW intialisation
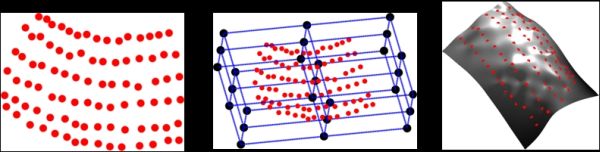
From the point tracks we extract a mean 3D shape using a rigid SfM procedure (left figure). In this way, it is possible to reconstruct an initial template of the 3D deforming body. So we do not have to provide an explicit template manually which can be a difficult task in most real examples.Then we place a set of control points around the 3D shape (black dots) and we build the 3D warping function directly in the 3D metric space (central figure). In this way we are able to impose multiview relations between the 3D warp and the image correspondences in the video. Differently, classical Image warps are in general restricted to pairwise image relations.
It is then possible to augment the 3D shape with a dense surface obtained by simple interpolation (right figure). When the dense mesh is reprojected into the image plane (green dots) it models the image deformation given the learned 3D warps.
M3DW estimation
The estimation of the M3DW given a set of 2D image trajectory is formulated as an optimisation problem with non-linear constraints given by the camera projection into the image plane. Details can be found in the paper (section 4), in the following we provide a visualization of the main steps. Given the 3D warp function and the multiview relations, we can define the M3DW model as:
where:
- The matrix
contains the 2D image points that can be partitioned at each frame such as:
;
- The matrices
and
defines the 3D warp given the initialised 3D template;
- The matrix
contains the 3D control points displacement which model the object shape deformations. The control points position at each frame is given by
;
- The block-diagonal matrix
map the 3D motion of the control points (and thus the deformations) into the video sequence.
Modelling the image deformations results in estimating the control points displacement and the camera projection matrices (a simple orthographic camera model here). The associated cost function is the following:
where the equality constraints refers to an orthographic camera model at each frame
. The matrix
masks the missing data in the 2D image trajectories The solution is given by an Augmented Lagrangian Multipliers (ALM) method for matrix factorisations called the BALM.
M3DW applications
Shape augmentation: Given the sparse template obtained by rigid SfM, we augment the shape by surface interpolation obtaining a dense 3D mesh. Given the 3D mesh and the learned warping functions it is possible to map the dense deformation field in the video sequence.
Deformation cloning: The learned deformation field is independent of the imaging conditions (i.e. the camera pose) and the shape motion. Thus the learned dense warp in the metric space can be easily reused to augment a new sequence or to transform the existing one.
The original surface in blue shows the original deformation estimated from a video sequence. The smaller red mesh is cloned from the original but resized by two and rotated.
Image Retexturing: The video shows the retexturing of the paper image sequence where a synthetic texture is added to the bending paper. Notice that the augmentation is made by first projecting the dense mesh obtained in augmentation and then by retargeting the texture to augment the video with the ICCV 2011 logo.
-
A. Del Bue and A. Bartoli, "Multiview 3D Warps," in 13th Internationl Conference on Computer Vision (ICCV 2011), Barcelona, Spain, 2011.
@inproceedings{DelBue:Bartoli:2011,
author = {A. {Del Bue} and A. Bartoli},
title = {Multiview 3D Warps},
booktitle = {13th Internationl Conference on Computer Vision (ICCV 2011), Barcelona, Spain},
year = {2011},
month = {November}
}





[...] M3DW – Multiview 3D Warps [...]
[...] M3DW – Multiview 3D Warps [...]