Robot Navigation and Multi Robot Task Allocation

Our work is broadly situated at the intersection of mobile robots and sensor networks. The underlying principle in interaction between the network and robots is: the network serves as the communication, sensing and computation medium for the robots, whereas the robots provide actuation (mobility), which is used among other things for network deployment, repair, and other tasks. In this work we use a new Networked Infomechanical Systems (NIMS) architecture that combines both static and mobile sensor nodes. This architecture achieves a spatiotemporal environment coverage that is dramatically advanced over that of either system alone. Mobility allows the networked sensor system to always seek the spatiotemporal sampling distribution to achieve a specified fidelity of environmental variable reconstruction. We demonstrate that mobility permits the NIMS system to respond to initially unpredictable and variable environmental evolution. In our work static sensor nodes are positioned in the volume surrounding a transect in which the mobile node operates. Every sensor node is responsible for reporting a phenomenon occurring in the vicinity. The mobile node then uses simple task allocation to determine which node has higher priority and then can utilize sampling algorithms (either raster or adaptive sampling) to sample only the vicinity of the node that detected the phenomenon. In our previous work we experimentally showed the benefits of such a stratification of the sampling transect. The rapid time rate of change of field variable value leads to a need for even higher performance in the response of the mobile sensing system to environmental events. We introduce two new Task Allocation algorithms used by NIMS and present the results of performance analysis obtained directly in the field and operating in the forest reserve. In some cases, additional performance analysis is obtained from measurements on a physical testbed duplicate of NIMS that includes sensor data records obtained from the field. This permits reproducible, repeated measurements of the same events for a probe of system performance.

Network Deployment using Robots

The ability to self-deploy and self-configure is of critical importance for mobile sensor networks because of the unattended nature of intended applications. The network should be able to dynamically adapt its topology to meet application-specific requirements of coverage and connectivity. In static networks topology control is achieved by controlling the transmission power or sleep/wake schedules of nodes that are densely deployed. In contrast, mobile sensor networks can exploit control over node positions to affect network topology thus eliminating the need for over-deployment and increasing the net area sensed. A key challenge in achieving this is that desired network properties are typically global in nature (for example, degree of connectivity of a network) while the nodes can only sense and act locally. Our project focuses on understanding local properties that control the global network topology and using these to design control laws for self-deployment of mobile networks.

APPROACH

Multi-Robot Task Allocation using a Sensor Network

Task Allocation (TA) is the problem of assigning available resources to tasks. There are two major subdivisions: offline and online. Offline TA is the problem of assigning resources to tasks if certain information (e.g. the distribution of task arrival times, relative task priority) is known a priori. The assignment process proceeds offline. The offline TA problem, in its most general form, is equivalent to the conjunctive planning problem which is NP-Complete.

Our focus is on online task allocation. In online TA, all information about the tasks becomes available only upon task arrival. The assignment of resources to tasks must be computed in real time. It has been shown that greedy algorithms provide good approximate solutions to online TA. It has also been shown that in some cases the greedy online TA solution is within a bounded limit of the optimal solution obtained by offline TA. We think of task assignment occurring in decision epochs. A decision epoch is a period of time during which only the tasks, which have arrived since the end of the previous epoch, are considered for assignment. Increasing the decision epoch to infinity converts the online TA into the offline TA problem. We model the NIMS system as an online TA problem, since it is designed for real-life autonomous field applications in dynamic environments.

Our work is related to the body of work on the problem of online multi-robot task allocation (MRTA). The proposed TA algorithm differs from existing MRTA approaches. It relies on a static network, and communication, sensing, and computation are distributed. The motivation for the TA algorithm derives from the need to efficiently sample the phenomena instead of the entire environmental space. As has been discussed in the introduction, it is impractical to deploy sufficient numbers of fixed sensors to achieve required sensing fidelity. As will be shown, the system combining fixed and mobile nodes enables efficient sampling. TA becomes the primary driver of efficient data collection in this system, since it allows the user to select a subset of the environment for sampling, as opposed to sampling the entire environment. In addition, TA manages system resources, so that resources are not consumed unless assigned most effectively.

Methodology

The general online TA system functions in the following way. Suppose at a given decision epoch the system maintains a set of resources R = {r₁, ..., r_n} and tasks T = {t₁, ..., t_k}. Tasks are prioritized based on a criterion C. C is an application dependent function and can combine such parameters as task arrival time, task importance, etc. A set of assignments A = (l = min(n,k): {a₁, ..., a_l}) is computed as follows:

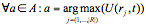
where t is the next unassigned task according to C and U(r_j,t) is the j-th resource utility value for accomplishing t. The assigned resource and corresponding task are removed from R and T respectively, before the next assignment. The utility function is chosen to be application and resource dependent. In our model, once assigned, resources cannot be reallocated. After a resource has completed its task it becomes available for a new assignment. We adopt a commitment as opposed to an opportunism strategy.

The system consists of a mobile node suspended on a cable and a static sensor network. We assume that the network is predeployed where each node knows its location in a global coordinate system. The network monitors the environment for events of interest (motion, change in light intensity, etc). The problem then is to prioritize the events, and drive the mobile node to a vantage point from which a particular event is better observed. Once the node arrives at the event location, the local phenomenon is measured.

terminology, a robot is a resource and a detection by a sensor node of an event requiring perusal by a robot is a task.

Figure 1 shows two network topologies that we define - positioned on the ground (the 2D-case) and more generally, in the volume surrounding the transect (the 3D-case). In order for the TA system to plan the node's motion the goal points should lie in the transect plane. Hence, we project the nodes locations onto the transect plane. As a result we get a set of points on a line l (2D-case, Figure 1a) or a plane ¹_r (3D-case,

Figure 1c), both of which lie in the transect plane. In the 2D-case, l is the line where the transect plane intersects the ground plane. Since, the mobile node cannot move along that line, we translate l to a parallel line l_r on the transect. We define the projection function in the 2D-case PROJ_lr and 3D-case PROJ _¹r.

Based on tasks projected locations TA divides the transect into slices (2D-case, Figure 1b), or generally cells (3D-case, Figure 1d). With every projected node k we associate a cell C_n.

Note that a 2D system is sometimes preferred because it is easier to setup in the field and for some applications a 2D perspective is enough. As an example, consider studying sunlight intensity shining through a forest canopy. In this case a sensor network with illumination detectors can be placed on the ground. Suppose node k discovered an interesting reading (say an abnormal light value). The TA system then would guide the robot towards the goal point on l_r  computed by PROJ_lr. The mobile node then can study appropriate slice C_k. We assume the general 3D-case system.

The Task Allocation System

Our system is a special case of the TA methodology described above - with only one resource (mobile node) for task assignment. We consider the problem of assigning tasks one at a time. In this case the greedy assignment is obviously optimal. Consider task assignment Equation 1. Since there is only one mobile node, the next task with highest

priority (according to criterion C) is assigned to the mobile node, no matter what the mobile node's utility function might be. In our work we consider two basic greedy policies, one based on a task's arrival time (we term it the time policy) and another based on the distance to the task (we term it the distance policy). In our system these policies essentially define the task prioritization criterion C.

The Task Allocation system consists of two algorithms, one running on the static sensor nodes and the other on the mobile node. The algorithm of static nodes is simple - retrieve data from the sensors, process it, and deliver to the mobile node via a wireless link.

The algorithm running on the mobile node is as follows. Suppose the mobile node receives the sensor data from the static node i. This data is analyzed and if there is a difference greater than a threshold in the current sensor data with respect to the previously stored value, a sampling task for the sensor node i is created. The task for the robot is then to travel to the location of the node that generated the task (after that a sampling policy can be applied to the vicinity of the static node, but this is not our focus here). Next, if the task generated by node i is not stored in a set of currently active tasks T_a, it is added to this set. If the mobile robot is available for the next task and T_a ­ 0, the next task is extracted from T_a according to the criterion C. We implemented two policies for the criterion C - time policy (tasks with smaller time stamp get priority) and distance policy (tasks closer to the robot get priority). Note that since the system does not have any priori knowledge about the spatiotemporal variation of event arrival, simple greedy scheduling (time and distance) is appropriate. In our future work, as we will learn more about the nature of the phenomenon, we plan to incorporate that knowledge into the task allocation process. Next, based on the task information the mobile node needs to compute a goal point. If the task's position is p then the goal position will be PROJ_lr (p) in 2D-case and  PROJ _¹r (p) in 3D-case (see Figure 1). The robot then moves to the computed location of the task. After the robot completes its last task it becomes available for reassignment.

We have explored two approaches to this problem. One is based on heuristics with minimal assumptions on the sensing and communication capabilities of nodes. In the second approach we assume that nodes have ideal disc like communication ranges and use this analyze the geometric properties of network topologies.

In prior work, we developed a potential field based deployment algorithm for mobile nodes that maximized coverage with the constraint that each node has at least k neighbors where k is a user-defined parameter. The algorithm used two kinds of potential forces – a repulsive force that causes the nodes to move away from each other to maximize coverage and an attractive force that constrains the node degree. By using a combination of these forces, each node can maximize its coverage while maintaining at least k neighbors. While there is a strong correlation between average node degree and connectivity of a network, we cannot guarantee that the network will be connected.

To address the problem of connectivity, we developed a simple algorithm where the nodes broadcast heartbeat signals to their neighbors at a regular rate. In particular, a single node is chosen as the Òreference nodeÓ (ex: Node with the smallest id) that starts the heartbeat and every node that can hear it begins to broadcast a heartbeat.  As a result, the nodes form a tree with the reference node as the root. A repulsive potential field is used to maximize coverage so that the nodes move away from each other while ensuring that a satisfactory level of connectivity (ex: signal strength of incoming messages) is maintained.

This algorithm is completely asynchronous and distributed. In addition, it is well suited for real radios that are notoriously irregular. The total number of messages is bounded by f*T per node where f is the frequency of the heartbeat and T is the deployment time. Though the total number of message exchanges is large, these messages can be easily piggy-backed onto other messages so that the additional communication cost for deployment is minimized.

In our second approach, we model the communication network as a disc-graph and derive local conditions that can guarantee network-wide properties. In particular, we have focused on proximity graphs such as the Relative Neighborhood Graph, Gabriel Graph, etc that are known to have desirable properties in terms of connectivity, sparseness and efficient communication paths (spanner properties).  We have shown that regularly tiled graphs maximize coverage in addition to providing desirable connectivity properties. We have developed simple local rules that can guarantee the formation of the above proximity graphs. In this case, we assume that the nodes can sense the positions of their neighbors relative to themselves.