Discrete Event Systems simulation
using Petri nets with inputs
2013, José Gaspar
Introduction
In this page you can find a
Petri nets simulator to use in Matlab. In particular this page contains a
complete functional example of simulating the well know "philosophers
dinner" problem. This simulated discrete event system serves as a basis
example for the laboratory of the Industrial
Automation Course 2013/14.
The reason for teaching in
the course Petri nets with input/output is that it is a way of designing
programs for PLCs. The direct implementation for a PLC is not considered in
this webpage. The focus here is the simulation of the complete system.
Running a Petri net
requires a simulator of a system to interact with or, in other words, to
supervise. In particular are required interface functions (IO) of the Petri net
with the system to interact with. See in figure1 the arrows "PN
actuation" meaning the outputs required to drive the system, and see "PN
inputs" meaning the signals observed in the system and used to drive the
Petri net.
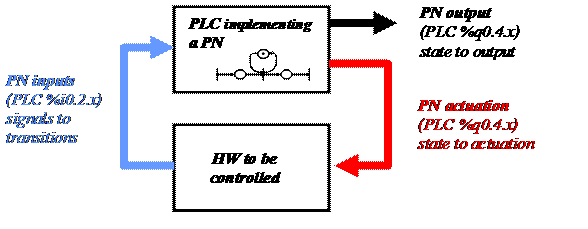
Figure1: Petri net supervising the system "HW to be
controlled".
The simulation of a Petri
net consists of two main steps namely (i) the verification that the
pre-conditions are met and (ii) the state evolution after selecting just the
possible-to-fire events. See in figure2 an implementation using Matlab.
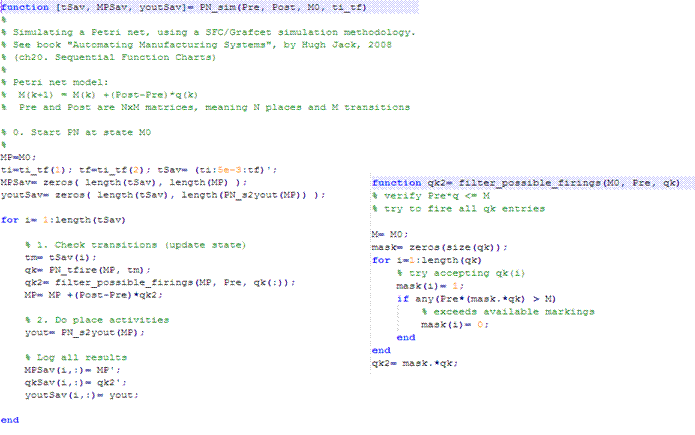
Figure2: Running a Petri net.
Interacting with the system
to be supervised by the Petri net involves defining inputs and outputs. In the
simulator, the inputs and the outputs are handled by two functions having
predefined names "PN_s2act.m" and "PN_tfire.m". A working
example encompassing inputs is made available in the next section and described
in a later section.
Download and Usage
Download the zip file lab2_sim_5philosophers.zip and decompress
it to a folder of your choice (note, this code is the version updated in 2015 to
correct for a display issue). Download also the Petri
Nets Toolbox by Zdenek Hanzalek and Martina Svadova and add it to the path.
To run the main demo:
>>
pdinner_tst
Downloaded Example Explained
The main demo loads a Petri
net model shown in figure3 and built using PMEDIT. The firing of the
transitions is regulated by signals described in the next paragraphs.
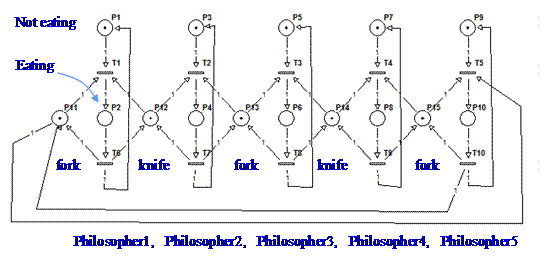
Figure3: Petri net model representing the 5 philosophers dinner problem.
Firing transitions of the
Petri net corresponds to having the philosophers issuing requests to eat. In
the current simulation these requests are time signals described in a script.
The script, more precisely a Matlab function, is run at each time stamp which,
according to the time stamp, return an array of flags where is philosopher is
indicated his desired to eat or not. See in figure4 part of the script and a
graphics representation of the time signals.
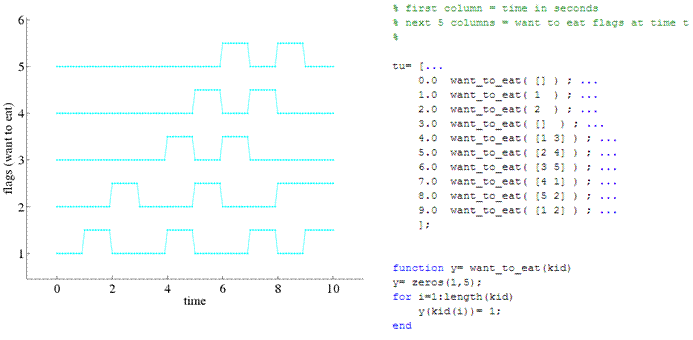
Figure4: Requests to eat issued by the philosophers.
The Petri net answers positively when a philosopher can get both the fork and
the knife.
Given the input signals,
the running of the Petri net shows which philosophers can be effectively eating
at each time (see figure5). In case of a real system, where various subsystems
are requiring access to shared resources, the Petri net would be indicating at
each moment which subsystems are allowed to use the resources without
conflicting with others.
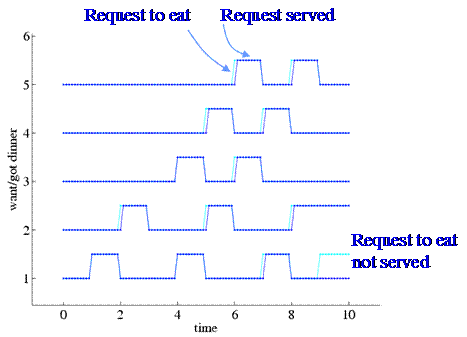
Figure5: Served requests to eat.
Note that modern operating
systems must work better than failing early like in this simulation. The most
common solution is to change the Petri net to not receive directly requests
but, instead, to have a resources manager, which tries at all times to have the
largest possible number of clients served.
Maintenance
This program was created
for the purpose of helping classes. There is no continuous maintenance other
the requirements associated to the classes.
This program is distributed
in the hope that it will be useful, but without any warranty; without even the
implied warranty of merchantability or fitness for a particular purpose.
Acknowledgment
In case you find this
software useful and do any publication in the sequel please refer to the course
Industrial
Automation.
Contact
|
Prof. José Gaspar Instituto de Sistemas e Robótica, Instituto Superior Técnico, Torre Norte Av. Rovisco Pais, 1 1049-001 |
Office: Torre
Norte do IST, 7.19 |