Exemplo de Utilização do PSPICE:

Rede Resistiva

Fev08, Jan09 - JGaspar

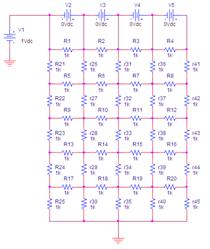
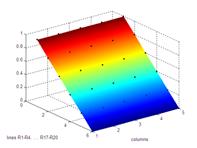
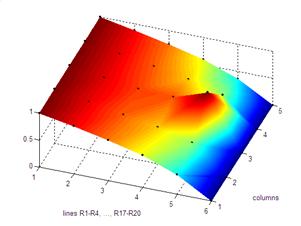
Esta experiência tem por objectivo fundamental ilustrar o conceito de "potencial eléctrico". Neste sentido toma-se por ponto de partida uma matriz de resistências, ligadas à terra por um lado e ligadas a um potencial de 1V no lado oposto. Cria-se desta forma um campo de potenciais (tensões nodais) com a forma de uma "rampa" - ver figura 1. Variando as tensões de alimentação podem ser obtidos vários gráficos de potencial.

(a)

(b)

(c)

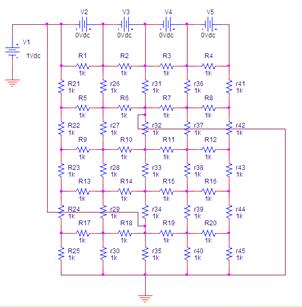
Fig.1: Rede resistiva (a), resultados após simulação com PSPICE (b), e resultados visualizados em Matlab (c).

1. Como realizar a simulação do circuito

Nesta secção assume-se que estão instalados o programa de simulação de circuitos PSPICE (a versão estudante é freeware) e uma ferramenta de cálculo matricial Matlab (c) ou Octave (freeware; 35Mb binário para Windows).

A simulação do circuito e a visualização do campo de potenciais (tensões nodais) realiza-se pelos seguintes passos:

a) Descomprimir para uma directoria o ficheiro seguinte (clicar para realizar o download):

rede_resistiva.zip

b) Abrir o ficheiro "rede_resistiva.opj" com o programa Capture incluído no PSPICE

c) Simular o circuito no menu do Capture "pspice -> run" ou então clicar no icon com o nome "Run pspice". Ter o cuidado de gravar previamente o circuito, para garantir que todos os valores visualizados pelo Capture são utilizados na simulação do circuito, e ter o cuidado de clicar no icon de "Run pspice" tendo seleccionada a janela de projecto (".opj") e não a janela do circuito.

d) Visualizar a representação gráfica das várias tensões nodais do circuito utilizando o programa Matlab ou Octave:

>> cd c:\directoria\onde\foi\descomprimido\o\zip

>> rede_resistiva_mostrar_tensoes

Nota técnica: por razões de facilidade de visualização a representação gráfica realiza uma interpolação das tensões nodais que para o PSPICE, e na prática profissional usual, não existe. O PSPICE considera a rede resistiva apresentada formada por resistências perfeitas, e que têm portanto parâmetros concentrados. Os parâmetros concentrados implicam que as resistências têm comprimento nulo e realizam portanto quedas abruptas de tensão, não havendo portanto lugar a interpolação das tensões nodais.

2. Mais experiências alterando valores das fontes

Na experiência original somente a fonte de tensão V1 tem uma tensão não nula. Como V2..V5 têm tensões nulas, os potenciais aos terminais destas fontes são todos iguais e coincidem com o valor estabelecido pela fonte V1.

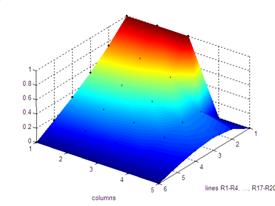
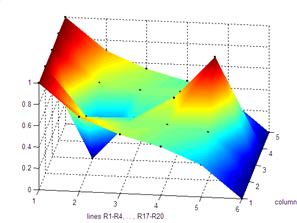
Colocando por exemplo V4=-1V, mantendo V1=1V e V2=V3=V5=0V, então os potencias aos terminais das fontes V2..V5 já não são todos iguais. Por exemplo os terminais de V5 estão a um potencial superior em 1V em relação aos potenciais de V2 e V3. Nestas condições o gráfico de potenciais nas resistências já não é uma rampa. Ver figura 2.

(a)

(b)

Fig.2: A tensão V4 é nesta experiência -1V (valia zero). O gráfico obtido em Matlab deixa portanto de ser uma rampa.

3. Mais experiências alterando topologia do circuito

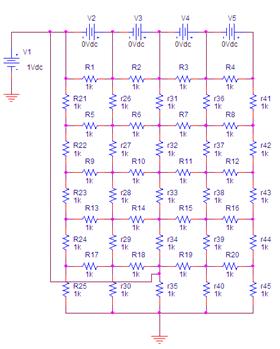
Alterando a topologia do circuito podem-se manipular individualmente as várias tensões nodais do circuito. Pode-se por exemplo colocar um pico no meio da rampa. Ver figura 3.

(a)

(b)

Fig.3: Circuito alterado de forma a que V1 afecta um dos nós interiores da malha (a). No gráfico dos potenciais verifica-se imediatamente o aparecimento de um pico no meio da superfície (b).

No exemplo anterior foi alterado o potencial de um dos nós interiores da rede. A alteração colocou um pico, máximo local, nos potenciais da rede. No exemplo seguinte alteram-se os potenciais de dois nós, um é alterado para um máximo local, tal como no exemplo anterior, e o outro potencial é alterado para constituir um mínimo local.

(a)

(b)

Fig.4: Dois nós interiores da rede são actuados por um valor de tensão máximo positivo, e por um valor nulo (a). O gráfico de Matlab mostra as deformações provocadas pelos dois pontos de tensão inseridos no interior da rede (b).