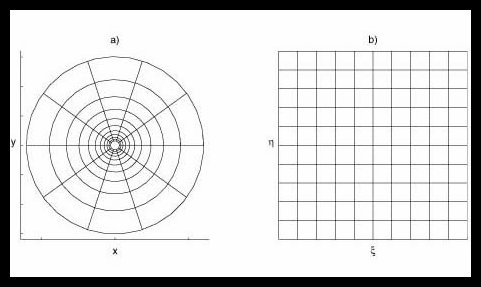
The log-polar image geometry was first motivated by its resemblance with the structure of the retina of some biological vision systems and by its data compression qualities. When compared to the usual cartesian images, the log-polar images allow faster sampling rates on artificial vision systems without reducing the size of the field of view and the resolution on the central part of the retina (fovea). In the last years, however, it has been noticed that the log-polar geometry also provides important algorithmic benefits. For instance in [AlexTRA99], it is shown that the use of log-polar images increases the size range of objects that can be tracked using a simple translation model. We expect that increasing the ``order" of the transformation towards the planar model, these advantages can still be observed.
The log-polar transformation is a conformal mapping from the points on the cartesian plane (x,y) to points in the log-polar plane (x,h):

The mapping is described by:
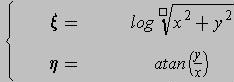
The system described in this pages is based on a log-polar space variant image sampling. One advantage of this kind of sampling is data reduction. This is obtained by reducing the resolution at the image periphery, thus high resolution in the fovea improves the performance of the tracking process. We map 128x128 cartesian images to 64x32 log-polar images and achieve 8 times increase in efficiency (both storage and speed):
Cartesian image ----- Log-Polar representation ----- Retinal representation

![]()

For tracking, the main advantage of the log-polar geometry is that
objects occupying the central high resolution part of the visual field become dominant over coarsely sampled background elements in
the image periphery. This embeds an implicit focus of attention in the center of the visual field where the target is expected to be
most of the time.